
RVP8 User’s Manual
March 2006
Processing Algorithms
5. Processing Algorithms
Note: Optional dual polarization processing algorithms are described in Appendix B.
This chapter describes the processing algorithms implemented within the RVP8 signal processor.
The discussion is confined to the mathematical description of these algorithms. Figure 5–1
shows the overall process by which the RVP8 converts the IF signal into corrected reflectivity,
velocity, and width. Table 5–1 summarizes the quantities that are measured and computed by the
RVP8. The type of the quantity (i.e., real or complex) is also given. Subscripts are sometimes
used to denote successive samples in time from a given range bin. For example, s
“I” and “Q” time series or “video” sample from the n’th pulse from a given range bin. In cases
where it is obvious, the subscripts denoting the pulse (time) are dropped. The descriptions of all
the data processing algorithms are phrased in terms of the operations performed on data from a
single range bin- identical processing then being applied to all of the selected ranges. Thus, there
is no need to include a range subscript in this data notation.
denotes the
n
It is frequently convenient to combine two simultaneous samples of “I” and “Q” into a single
complex number (called a phaser) of the form:
s + I ) jQ
where “j” is the square root of –1. Most of the algorithms presented in this chapter are defined in
terms of the operations performed on the “s”’s, rather than the “I”’s and “Q”’s. The use of the
complex terms leads to a more concise mathematical expression of the signal processing
techniques being used. In actual operation, the complex arithmetic is simply broken down into
its real-valued component parts in order to be computed by the RVP8 hardware. For example,
the complex product:
s + W Y
is computed as
Real{s}+ Real{W}Real{Y}* Imag{W}Imag{Y
Imag{s}+ Real{W}Imag{Y}) Imag{W}Real{Y
where “Real{}” and “Imag{}” represent the real and imaginary parts of their complex-valued
argument. Note that all of the expanded computations are themselves real-valued.
In addition to the usual operations of addition, subtraction, division, and multiplication of
complex numbers, we employ three additional unary operators: “||”, “Arg” and “*”. Given a
number “s” in the complex plane, the magnitude (or modulus) of s is equal to the length of the
vector joining the origin with “s”, i.e. by Pythagoras:
}
}
| s | + Real{s
The signed (CCW positive) angle made between the positive real axis and the above vector is:
ë+Arg{s}+ arctan
Ǹ
}
5–1
2
) Imag{s
Imag{s
ƪ
Real{s
2
}
}
ƫ
}

RVP8 User’s Manual
March 2006
Processing Algorithms
where this angle lies between * p and ) p and the signs of Real{s} and Imag {s} determine
the proper quadrant. Note that this angle is real, and is uniquely defined as long as |s| is
non-zero. When |s| is equal to zero, Arg{s} is undefined. Finally, the “complex conjugate” of “s”
is that value obtained by negating the imaginary part of the number, i.e.,
s*+ Real{s}* jImag{s}.
Note that Arg{s*} = –Arg{s}. The reader is referred to any introductory text on complex
numbers for clarification of these points.
Table 5–1: Algebraic Quantities Within the RVP8 Processor
p Instantaneous IF-receiver data sample Real
b Instantaneous Burst-pulse data sample Real
I,Q Instantaneous quadrature receiver components Real
s Instantaneous time series phaser value Complex
sȀ Time series after clutter filter Complex
T
0
R
0
R
1
R
2
Zeroth lag autocorrelation of A values Real
Zeroth lag autocorrelation of AȀ values Real
First lag autocorrelation of AȀ values Complex
Second lag autocorrelation of AȀ values Complex
SQI Signal Quality Index Real
V Mean velocity Real
W Spectrum Width Real
CCOR Clutter correction Real
LOG (Signal+Noise)/Noise ratio for thresholding Real
SIG Signal power of weather Real
C Clutter power Real
N Noise power Real
Z Corrected Reflectivity factor Real
T UnCorrected Reflectivity factor Real
The following sections cover the various parts of the diagram shown in Figure 5–1, i.e.,
S IF Signal Processing
S I/Q processing and clutter filtering
S Range averaging and clutter microsuppression
S Moment calculations (reflectivity, velocity, spectrum width)
S Thresholding for data quality and Speckle Filtering
S Reflectivity Calibration
S Special algorithms for ambiguity resolution (dual PRF, dual PRT, Random Phase)
S Calibration and Testing
5–2
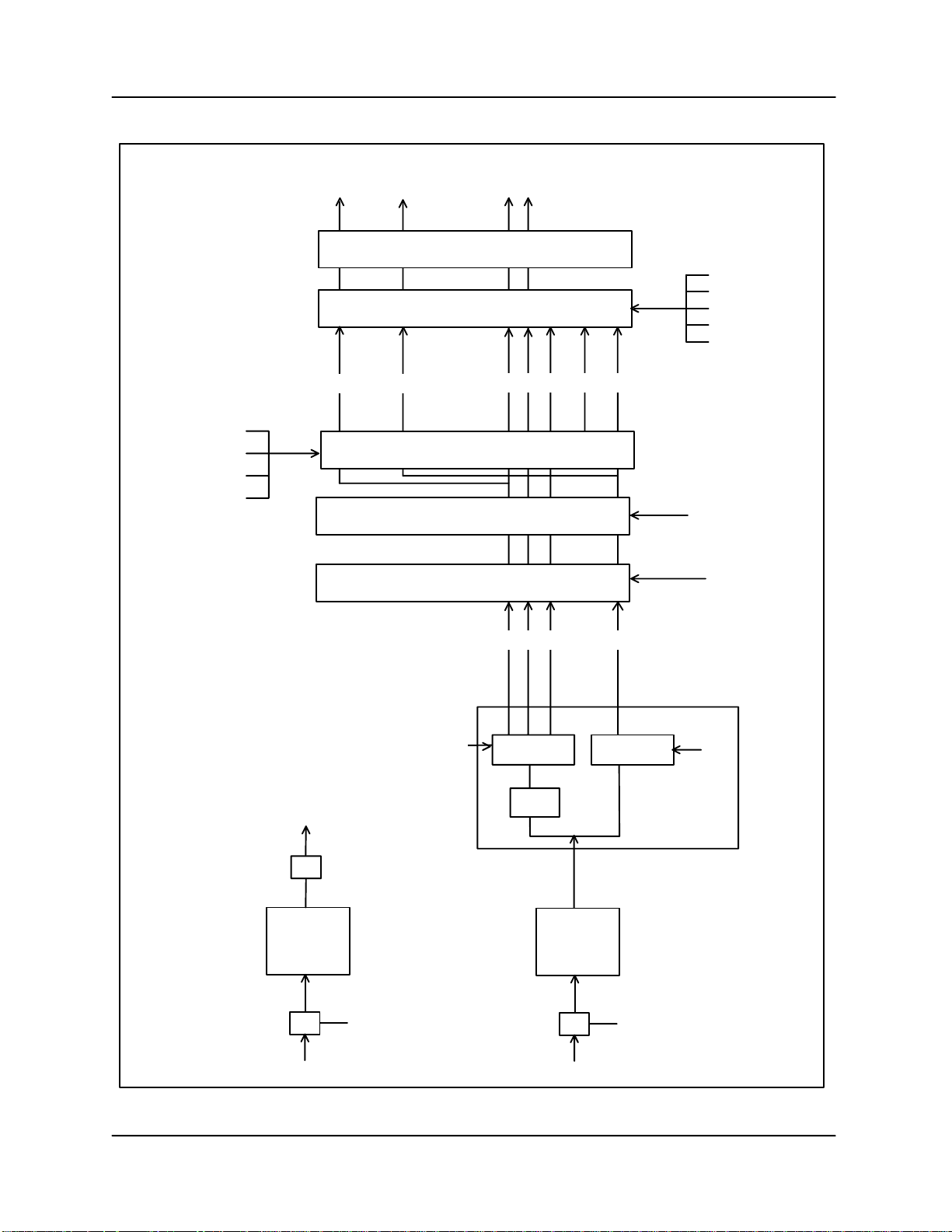
RVP8 User’s Manual
March 2006
Figure 5–1: Flow Diagram of RVP8 Processing
dBZ
dBT
Speckle Remover
Thresholding
V W
Processing Algorithms
SIG
TH
LOG
TH
SQI
TH
CCOR
TH
FLAGS
dBZ dBT
N
Calibrate Moments
l
dBZ
0
Calculate Output Data
a
Range Averaging
Micro Clutter Suppression
Clutter Filtering and Autocorrelation by
Time Domain or Frequency Domain Approach
M
AFC
V W SQI SIG CCOR
R0 R1 (R2) T
Correlate Correlate
Filter
K–bins
CCOR
TH
0
M
D/A
FFT
Compute
Frequency
A/D
36 MHz
Burst IF Input Channel
s
i
FIR
Decimate
in Time
A/D
IF Signal Input Channel
5–3
(I and Q)
36 MHz

RVP8 User’s Manual
March 2006
Processing Algorithms
5.1 IF Signal Processing
The starting point for all computations within the RVP8 are the instantaneous IF-receiver
samples p
available at a very high sampling rate (typically 36MHz), which makes possible the digital
implementation of functions that are traditionally performed by discrete components in an
analog receiver. The RVP8’s all-digital approach replaces a great deal of analog hardware,
avoids problems of aging and maintenance, and makes it easy to tune-up the receiver and alter
its parameters.
This section describes these IF signal processing steps. Please refer to Figure 1-3 for a block
diagram of the IF processing that is performed.
5.1.1 FIR (Matched) Filter
The RVP8 implements a digital version of the “matched” filter that is found in the traditional
analog radar receiver. The equivalent Finite-Impulse-Response (FIR) filter is designed using an
interactive graphical procedure described in Section 4.4. The filter length (number of taps),
center frequency, and bandwidth are all adjustable. The design procedure computes two sets of
filter coefficients f
where N is the length of the filter. The input samples pn are centered on the range bin to which
the (I, Q) pair is assigned. Note that some of the p
i.e., the filter length may be chosen to be greater than the bin spacing. Such an overlap
introduces a slight correlation between successive bins, but the longer length allows a better
filter to be designed.
and, the instantaneous burst-pulse or COHO reference samples bn. These data are
n
i
and f
n
q
such that the instantaneous quadrature samples at a given bin are:
n
I +
N*1
ȍ
n+0
i
f
pn, Q +
n
N*1
q
ȍ
f
p
n
n
n+0
are likely to overlap among adjacent bins,
n
The sums above for I and Q are computed on the RVP8/Rx board using dedicated FIR chips (for
revisions A and B) that can perform up to 576 million sums of products per second. The Rev C
RVP8/Rx uses a more flexible FPGA. The p
i
f
and f
n
q
are represented as 10-bit (Rev.A/B) or 16-bit (Rev.C) signed integers. A numerical
n
are represented as 16-bit signed integers, and the
n
optimization procedure is used to quantize the ideal filter coefficients into their hardware values.
The overall spectral purity of the FIR filter will typically be greater than 66dBc (Rev.A/B) and
84dBc (Rev.C).
The reference phase for each transmitted pulse is computed using the same two FIR sums,
except with b
substituted for the pn. For a magnetron system the Nbn samples are centered
n
on the transmitted burst; for a Klystron system they may be obtained from the burst pulse
(recommended) or from the CW COHO. If the Klystron is phase modulated by an external
phase shifter (as opposed to the RVP8/Tx digital transmitter board), then the samples should be
from the modulated COHO.
i
The f
coefficients are computed as:
n
i
f
+ ln sin
n
p
ƪ
4
) 2p
f
f
SAMP
ǒ
n *
5–4
N * 1
2
Ǔ
ƫ
, n + 0 AAA N * 1
IF

RVP8 User’s Manual
March 2006
Processing Algorithms
where fIF is the radar intermediate frequency, f
frequency, and l
are the coefficients of an N-point symmetric low-pass FIR filter that is
n
matched to the bandwidth of the transmitted pulse. The multiplication of the l
is the RVP8/IFD crystal sampling
SAMP
terms by the
n
sin() terms effectively converts to the low-pass filter to a band-pass filter centered at the radar IF.
q
The formula for the f
The phase of the sinusoid terms, and the symmetry of the l
coefficients is identical except that sin() is replaced with cos().
n
terms, has been carefully chosen to
n
have a valuable overall symmetry property when n is replaced with (N–1)–n, i.e., the sequence is
reversed:
i
f
(N*1)*n
+ l
i
f
(N*1)*n
(N*1)*n
+ ln cos
sin
i
f
p
ƪ
) 2p
4
ƪ
(N*1)*n
p
4
f
SAMP
) 2p
+ f
f
IF
ǒ
((N * 1) * n) *
f
IF
ǒ
SAMP
q
n
n *
f
N * 1
2
Ǔ
ƫ
N * 1
2
Ǔ
ƫ
Thus, the coefficients needed to compute I are merely the reversal of the coefficients needed to
compute Q; if you know f
i
, then you also know f
n
q
.
n
5.1.2 RVP8/Rx Receiver Modes
The RVP8 supports six fundamental IFD and RVP8/Rx configurations which allow you to
choose the best style of IF processing for your particular site. The following table summarizes
the options where, BW is the net IF sampling rate (full 72MHz, or halfband filtered 36MHz),
DynR is the dynamic range (normal single channel, or extra wide dual channel), Pol is the
number of polarizations, Freq is the number of distinct intermediate frequencies, and IFD is the
number of IFD’s, along with their corresponding RVP8/Rx cards.
# BW DynR Filt Pol Freq IFD Description
– –––– –––– –––– ––– –––– ––– ––––––––––––––––––––––
0 Full Norm Norm 1 1 1 Standard single channel
1 Full Norm Norm 2 2 1 Dual Pol on two frequencies
2 Full Norm Norm 2 1 2 Dual Pol on separate IFDs
3 Half Norm Norm 2 1 1 Dual Pol on single IFD
4 Half Wide Norm 1 1 1 Extra wide dynamic range
5 Half Norm Long 1 1 1 Extra long/fast FIR filters
The first three modes were already supported in the previous RVP7 processor. The last three
modes are unique to the RVP8 and bring some exciting additional capabilities to the signal
processor. The six receiver modes are summarized below. Please see the Discussion of
Halfband Filtering (Section 5.1.2.1) as it applies to Modes 3-5, and the Discussion of Wide
Dynamic Range (Section 5.1.2.2)for additional details on using Mode-4.
Mode-0
: Standard Single Channel This is the most common “vanilla” mode that is used by
single-polarization CW-pulsed radars whose front-end LNA has a dynamic range less than
92dB. The (I,Q) data are computed from IF samples at their full acquisition rate (32MHz for
Rev.D IFDs, and 72MHz for Rev.F), and the resulting dynamic range from 14-bit IFD samples is
well matched to the RF components.
5–5

RVP8 User’s Manual
March 2006
Processing Algorithms
Mode-1: Dual-Pol On Two Frequencies This was the original dual-Pol configuration used by
the RVP7 several years ago. A single IFD A/D converter receives the “H” and “V” channels
using two distinct intermediate frequencies. Two different STALOs are required in this
configuration, making the RF/IF components a bit more expensive, but only one IFD is required.
Mode-2
: Dual-Pol On Separate IFDs This mode was introduced into the RVP8 in 2003, and
provides dual polarization data using two IFDs connected to two RVP8/Rx cards in the same PCI
chassis. A single intermediate frequency is used, hence only one STALO is required.
Mode-3
: Dual-Pol On Single IFD This is the recommended dual polarization mode for all new
RVP8 installations. The “H” and “V” channels are fed into the Primary and Secondary IFD
inputs using a single intermediate frequency. System cost and complexity are both optimized in
this design since only a single IFD, RVP8/Rx card, and STALO are required to process both
polarization channels.
Mode-4
: Extra Wide Dynamic Range Radars having very high performance front-end LNAs
can preserve the full benefit of that investment by running two separate IF signals into the
Primary (HiGain) and Secondary (LoGain) IFD inputs. A nominal channel separation of
25–30dB might be used to achieve an overall dynamic range of up to 110dB.
Mode-5
: Extra Long/Fast FIR Filters This mode is intended for pulse compression systems
that require unusually long filters (up to 80μsec), or finer range resolution in order to employ
higher compressed bandwidths without the risk of missing echoes between bins. For example, a
30μsec pulse could be processed at an incoming range resolution of 50 meters and then range
averaged down to 150meter output spacing.
5.1.2.1 Discussion of Halfband Filtering Modes 3-5
Traditionally, the IFD used by the RVP7 and RVP8 has sent raw 14-bit A/D samples from
its Burst and IF inputs directly to either the RVP7/Main or RVP8/Rx cards for FIR filtering
and conversion into complex (I,Q) values. The IFD would function simply as a waveform
sampling device (hence the acronym IF
Digitizer), and all of the front-end signal processing
took place downstream of it.
This model has changed with the introduction of the Rev.F IFD which has the ability to carry
out several billion multiply-accumulate cycles per second. This means that IF samples from
multiple signals can be preprocessed entirely within the IFD and then encoded without loss
onto the fixed bandwidth of its digital downlink. The new receiver modes 3 through 5 rely
on this hardware capability and use a method known as “Halfband Filtering” to effectively
double the downlink data rate.
Section 2.2.7 of the RVP8 User’s Manual contains a detailed account of how A/D quantization noise affects the dynamic range of the IFD. Briefly, for the Rev.F A/D converter which
runs at 72MHz, the contribution of A/D quantization noise within any given 1MHz interval
is 72 times smaller than the total noise of the converter itself. This is an important property
of all wideband sampling systems: the noise floor after processing, and hence the dynamic
range, are improved by increasing the fundamental A/D sampling rate.
Normally the IFD sends 72MHz A/D samples from a single input channel directly down to
the RVP8/Rx PCI card. The samples are sent at full speed in order to realize maximum reduc-
5–6

RVP8 User’s Manual
March 2006
tion of the final (I,Q) noise floor. But suppose we wanted to send two A/D waveforms down
the same data link by interleaving the samples together. Each channel would have to be
down-sampled to 36MHz in order to fit within this format, but that would cause its (I,Q)
noise floor to increase by 3dB.
To avoid this, we do not create the 36MHz streams merely by discarding every other A/D
sample, but rather, by passing the original 72MHz data through a halfband digital filter and
then discarding every other point of this filtered A/D stream. The difference is important.
Since the halfband filter has removed all of the A/D quantization noise from half of the original Nyquist interval, there will be no increase in noise density within the passband of the
(I,Q) filter when the halfband stream is down sampled to 36MHz. Thus, the A/D noise that
would normally have folded into the (I,Q) data at 36MHz is first removed by the halfband
filter so that we’re left with a 36MHz stream having the same dynamic range of the original
72MHz samples.
The IFD halfband filter is a 49-Tap equiripple FIR filter having 40dB of stopband rejection
and 0.175dB of passband ripple. The passband extends either from 0–16.5MHz when configured as a lowpass filter, or 19.5–36MHz when configured for highpass. The RVP8 automatically selects the correct type of filter depending on the intermediate frequency specified
in the Mb menu. The halfband filter has linear phase and is therefore non-dispersive. This
means that it is totally suitable for handling compressed pulses and other wideband Tx/Rx
waveforms.
Processing Algorithms
5.1.2.2 Discussion of Wide Dynamic Range Mode-4
When a two channel IFD is used as an extended dynamic range receiver there are some important decisions to make with respect to setting up the RF/IF levels that drive the IFD.
The first of these is the amount of signal level separation between the high gain and the low
gain IFD inputs. There is an absolute minimum and absolute maximum channel separation
that still allows the IFD to capture the full dynamic range of the receiver. If a signal level
separation is made that is outside of these absolute limits valuable receiver dynamic range
will be lost.
S The absolute minimum separation of the channels is equal to the total dynamic
range of the receiver minus the dynamic range of a single channel of the IFD.
Generally, the total dynamic range of the receiver is set by the LNA. For
example, if we are considering a 1μsec pulse (1MHz bandwidth), the dynamic
range of the LNA may be about 105dB, and the dynamic range of a single
channel of the IFD is about 84dB (from –78dBm to +6dBm). In this case, the
minimum separation would be 21dB. At minimum separation, the overlap of the
low gain channel and the high gain channel will be maximized, and that overlap
is equal to the dynamic range of a signal channel of the IFD minus the separation.
In this case, the overlap is ( 84dB – 21dB ) = 63dB.
S The absolute maximum separation of the channels is simply the dynamic range
of a single channel of the IFD. In the above example this would be 84dB. At
5–7

RVP8 User’s Manual
March 2006
maximum separation, the overlap of the low gain channel and the high gain
channel is zero -- we begin using one as soon as the other has begun to saturate.
We see that there can be a large difference between the absolute minimum and maximum
signal level separations; thus additional criteria must be considered to choose an optimum
value that is between these diverse limits.
Choosing a proper separation value is a tradeoff of several factors. If the separation value
is too low, the IFDs may end up operating very close to their noise floors. And if the separation is too high, then the overlap between the two channels is reduced which makes it dif ficult
for the IFD to make a smooth transition as it combines the data from both channels. Too high
a separation may also result in receiver components that are not practical to build.
As a rule of thumb, channel separations in the 22–30dB range provide a good balance of the
above criteria. In the case of a 1μsec pulse this results in an overlap interval of approximately
55-63dB, which is sufficient for good IFD transitions and also leads to receiver components
that are practical to build.
Once a separation value has been chosen, one must consider how to build the receiver to
achieve this. The basic receiver will take the form of an LNA and a mixer followed by a
splitter resulting in a low gain channel and a high gain channel. W e know the gain dif ference
in the two channels (the separation value), but we must find the actual gain to use in each
channel.
Processing Algorithms
If we consider the total system dynamic range as generally set by the LNA (105dB in the
above example), we can estimate the minimum detectable signal input to the LNA as well
as the maximum usable linear level at the IFD. If the LNA has a noise figure of 1dB and
we are using a 1μsec pulse, the minimum detectable signal at the LNA input is –113dBm,
and thus the maximum signal is 105dB above this, or –8dBm. If we add to these number
the gain of the LNA and the conversion loss of the mixer (and any other losses experienced
through the power splitter for the low gain and high gain channels), we can use this information to determine the signal values of the components in these two channels.
For example, if the LNA has a gain of 17dB, the mixer has a conversion loss of 7dB, there
is 1dB miscellaneous losses and 3dB loss in the power splitter, then the signal level at the
output of the power splitter is ( –113 + 18 – 7 – 1 – 3 ) = –106dBm for the minimum signal,
and and –1dBm for the maximum signal. In the low gain channel, we need to bring the
–1dBm up to the maximum input value of the IFD (+6dBm). To do this we need about 8dB
of amplification (7dB plus one more deciBel to account for the anti–alias filter loss of the
IFD). If we assume 25dB of channel separation, on the high gain channel we require about
+33dB of amplification. Finally , this tells us that on the low gain channel, the minimum and
maximum signals presented to the IFD are ( –106 + 8 ) = –98dBm and ( –1 + 8 ) = 7dBm.
For the high gain channel, the signal levels are ( –106 + 33 ) = –73dBm and ( –1 + 33 ) =
+32dBm. Note that as +32dBm is above the maximum input level tolerated by the IFD, the
amplifier on the high gain channel must limit its output to less than +16dBm. Thus an amplifier with an output saturation value of between +10dBm and +15dBm should be used.
5–8

RVP8 User’s Manual
March 2006
Processing Algorithms
5.1.3 Automatic Frequency Control (AFC)
AFC is used on magnetron systems to tune the STALO to compensate for magnetron frequency
drift. It is not required for Klystron systems. The STALO is typically tuned 30 or 60 MHz away
from the magnetron frequency. The maximum tuning range of the AFC feedback is
approximately 7MHz on each side of the center frequency. This is limited by the analog filters
that are installed just before the signal and burst IF inputs on the IFD. It is important that the
system’s IF frequency is at least 4MHz away from any multiple of half the digital sampling
frequency, i.e., 18, 36, 54, or 72MHz.
The RVP8 analyzes the burst pulse samples from each pulse, and produces a running estimate of
the power-weighted center frequency of the transmitted waveform. This frequency estimate is
the basis of the RVP8’s AFC feedback loop, whose purpose is to maintain a fixed intermediate
frequency from the radar receiver.
The instantaneous frequency estimate is computed using four autocorrelation lags from each set
of Nb
36MHz), but becomes noisy within 10% of each end. Since the span of the burst pulse samples
is only approximately one microsecond, several hundred estimates must be averaged together to
get an estimate that is accurate to several kiloHertz. Thus, the AFC feedback loop will typically
have a time constant of several seconds or more.
samples. This estimate is valid over the entire Nyquist interval (e.g., 18MHz to
n
Most of the burst pulse analysis routines, including the AFC feedback loop, are inhibited from
running immediately after making a pulsewidth change. The center-of-mass calculations are
held off according to the value of Settling time (to 1%) of burst frequency estimator, and the
AFC loop is held off by the Wait time before applying AFC (Mb Section 3.2.6). This prevents
the introduction of transients into the burst analysis algorithms each time the pulsewidth
changes.
Additional information about using AFC can be found in Sections 2.2.11, 2.4, and 3.2.6.
5.1.4 Burst Pulse Tracking
The RVP8 has the ability to track the power-weighted center-of-mass of the burst pulse, and to
automatically shift the trigger timing so that the pulse remains in the center of the burst analysis
window of the Pb plot. This means that external sources of drift in the timing of the transmitted
pulse (temperature, aging, etc.) will be tracked and nulled out during normal operation; so that
fixed targets will remain fixed in range, and clean Tx phase measurements will always be
available on every pulse.
The Burst Pulse Tracker feedback loop makes changes to the trigger timing in response to the
measured position of the burst. Timing changes will generally be made only when the RVP8 is
not actively acquiring data, in the same way that AFC feedback is held off for similar “quiet”
times. However, if the center-of-mass has drifted more than 1/3 the width of the burst analysis
window, then the timing adjustment will be made right away. Also, there will be an
approximately 5ms interruption in the normal trigger sequence whenever any timing changes are
made.
5–9

RVP8 User’s Manual
March 2006
Processing Algorithms
The Burst Pulse Tracker and AFC feedback loop are each fine-tuning servos that keep the burst
pulse “centered” in time and frequency. These servos have been expanded to include a
combined “Hunt Mode” that will track down a missing burst pulse when we are uncertain of
both its time and frequency. This coarse-tuning mode is especially valuable for initializing the
two fine-tuning servos in radar systems that drift significantly with time and temperature.
When the radar transmitter is On but the burst pulse is missing, it may be because either of the
following have happened:
S It is misplaced in time, i.e., the Tx pulse is outside of the window displayed in the Pb
plotting command. In this case, the trigger timing needs to be changed in order to bring
the center of the pulse back to the center of the window.
S It is mistuned in frequency, i.e., the AFC feedback is incorrect and has caused the burst
frequency to fall outside of the passband of the RVP8 anti-alias filters. In this case the
AFC (or DAFC) needs to be changed so that proper tuning is restored.
The Hunt Mode performs a 2-dimensional search in time and frequency to locate the burst;
searching across a +
20msec time window, and across the entire AFC span. If a valid Tx pulse
(i.e., meeting the minimum power requirement) can be found anywhere within those intervals
then the Burst Pulse Tracker and AFC loops will be initialized with the time and frequency
values that were discovered. The fine servos then commence running with a good burst signal
starting from those initial points.
Depending on how the hunting process has been configured in the Mb menu, the whole
procedure may take several seconds to complete. The RVP8’s host computer interface remains
completely functional during this time, but any acquired data would certainly be questionable.
GPARM status bits in word #55 indicate when the hunt procedure is running, and whether it has
completed successfully. The BPHUNT (Section 6.26) opcode allows the host computer to
initiate Hunt Mode when it knows or can sense that a burst pulse should be present
5.1.5 Interference Filter
The interference filter is an optional processing step that can be applied to the raw (I,Q) samples
that emerge from the FIR filter chips. The intention of the filter is to remove strong but sporadic
interfering signals that are occasionally received from nearby man-made sources. The technique
relies on the statistics of such interference being noticeably different from that of weather.
For each range bin at which (I,Q) data are available, the interference filter algorithm uses the
received power (in deciBels) from the three most recent pulses:
, P
P
n*2
where:
+ 10log
P
n
If the three pulse powers have the property that:
n*1
, and P
2
ǒ
I
n
10
) Q
n
2
Ǔ
.
n
Ť
P
* P
n*1
n*2
Ť
t C1 and ŤPn* P
5–10
n*1
Ť
u C2 (Alg.1)

RVP8 User’s Manual
March 2006
Processing Algorithms
then (In,Qn) is replaced by (I
n*1,Qn*1
). Here C1 and C2 are constants that can be tuned by
the user to match the type of interference that is anticipated, and the error rates that can be
tolerated. For certain environments it may be the case that good results can be obtained with
C
+ C2; but the RVP8 does not force that restriction.
1
This 3-pulse algorithm is only intended to remove interference that arrives on isolated pulses,
and for which there are at least two clear pulses in between. Interference that tends to arrive in
bursts will not be rejected.
Two variations on the fundamental algorithm are also defined. The CFGINTF command
(Section 6.23) allows you to choose which of these algorithms to use, and to tune the two
threshold constants. You may also do this directly from the Mp setup menu (Section 3.2.2).
Ť
P
* P
n*1
Ť
P
* P
n*1
Where LinAvg() denotes the deciBel value of the linear
n*2
n*2
Ť
t C1 and Pn* P
Ť
t C1 and Pn* LinAvg( P
n*1
u C2 (Alg.2)
n*1
, P
) u C2 (Alg.3)
n*2
average of the two deciBel powers. The
Alg.2 and Alg.3 algorithms also include the receiver noise level(s) as part of their decision
criteria. Whenever power levels are intercompared in the algorithms, any power that is less than
the noise level is first set equal to that noise level. This makes the filters much more robust and
properly tunable, so that interference is more successfully rejected on top of blank receiver
noise.
Optimum values for C
and C2 will vary from site to site, but some guidance can be obtained
1
using numerical simulations. The results shown below were obtained when the algorithms were
applied to realistic weather time series having a spectrum width = 0.1 (Nyquist), SNR = +10dB,
and an intermittent additive interference signal that was 16dB stronger than the weather. The
interference arrived in isolated single pulses with a probability of 2%.
Performance of the three algorithms is summarized in the first three columns of Table 5–2, for
which C
but with the value of C
and C2 have the common value shown. The fourth column also uses Algorithm #3,
1
raised by 2dB. The “Missed” rate is defined as the percentage of
1
interference points that manage to get through the filtering process without being removed. The
“False” (false alarm) rate is the percentage of non-interference points that are incorrectly
modified when they should have been left alone.
Table 5–2: Algorithm Results for +16dB Interference
Alg.1 Alg.2 Alg.3 Alg.3, C1+=2dB
C1,C2 Missed/False Missed/False Missed/False Missed/False
––––– –––––––––––– –––––––––––– –––––––––––– ––––––––––––
6.0dB 17.8% 10.91% 17.8% 4.06% 17.8% 3.48% 10.3% 4.15%
8.0dB 10.5% 6.57% 10.5% 2.42% 10.4% 1.71% 6.1% 1.92%
9.0dB 8.5% 5.09% 8.5% 1.81% 8.3% 1.16% 5.4% 1.28%
10.0dB 7.3% 4.01% 7.3% 1.42% 7.5% 0.79% 5.4% 0.85%
11.0dB 8.9% 3.14% 8.9% 1.06% 8.3% 0.51% 6.5% 0.54%
12.0dB 11.6% 2.53% 11.6% 0.85% 11.3% 0.33% 9.9% 0.35%
13.0dB 17.0% 2.07% 17.0% 0.67% 16.3% 0.22% 15.3% 0.23%
14.0dB 23.5% 1.70% 23.5% 0.54% 22.4% 0.14% 21.6% 0.15%
16.0dB 39.2% 1.21% 39.2% 0.35% 39.6% 0.06% 38.9% 0.06%
20.0dB 67.3% 0.65% 67.3% 0.14% 72.5% 0.01% 72.4% 0.01%
5–11

RVP8 User’s Manual
March 2006
Processing Algorithms
It is important to minimize both types of errors. If too much interference is missed, then the
filter is not doing an adequate job of cleaning up the received signal. If the false alarm rate is
too high, then background damage is done at all times and the overall signal quality (especially
sub-clutter visibility) may be compromised. We suggest that you try to keep the false alarm rate
fairly low, perhaps below 1%; and then let the missed percentage fall where it may.
To summarize the numerical results in Table 5–2:
S The “Missed” rates of Alg.1 and Alg.2 are identical, but the “False” rate of Alg.1 is
much higher. Alg.1 clearly does not perform as well for additive interference, but it is
included in the suite for historical reasons.
S The “Missed” error rate for Alg.3 is nearly identical to that of Alg.2, but Alg.3 has a
significantly lower false alarm rate. This is because of the somewhat improved statistics
that result when the linear mean of P
rather than just P
by itself. We recommend that Alg.3 generally be chosen in
n*1
n*2
and P
is used in the second comparison,
n*1
preference to the other two.
S Alg.3 can be further tuned by allowing the two constants to differ. For example, by
raising C
“Missed” rate for an increase in the “False” rate. Lowering C
slightly above C2 (fourth column), we can trade off a decrease in the
1
would have the opposite
1
effect.
Keep in mind that optimum tuning will depend on the type of interference you are trying to
remove. In the previous example, where the interfering signal is only 16dB stronger than the
weather, there was a close tradeoff between the “Missed” and “False” error rates. However,
Table 5–3 shows the results that would be obtained if the interference dominates by 26db.
Table 5–3: Algorithm Results for +26dB Interference
Alg.1 Alg.2 Alg.3 Alg.3, C2+=5dB
C1,C2 Missed/False Missed/False Missed/False Missed/False
––––– –––––––––––– –––––––––––– –––––––––––– ––––––––––––
6.0dB 17.8% 10.75% 17.8% 3.95% 17.8% 3.44% 17.8% 0.34%
8.0dB 9.9% 6.48% 9.9% 2.31% 9.9% 1.68% 9.9% 0.15%
9.0dB 7.4% 4.99% 7.4% 1.75% 7.4% 1.14% 7.4% 0.10%
10.0dB 5.9% 3.91% 5.9% 1.36% 5.9% 0.76% 5.9% 0.06%
11.0dB 4.8% 3.06% 4.8% 1.06% 4.8% 0.50% 4.8% 0.04%
12.0dB 3.2% 2.37% 3.2% 0.83% 3.2% 0.33% 3.2% 0.03%
13.0dB 2.6% 1.83% 2.6% 0.62% 2.6% 0.20% 2.8% 0.01%
14.0dB 1.9% 1.45% 1.9% 0.50% 1.9% 0.12% 2.6% 0.01%
16.0dB 1.3% 0.90% 1.3% 0.30% 1.3% 0.05% 5.8% 0.00%
20.0dB 3.1% 0.39% 3.1% 0.12% 2.0% 0.01% 31.5% 0.00%
Notice that we can now re-tune the constants and operate with C1+ 13dB and C2+ 18dB
(fourth column); which yields a low 2.8% “Missed” rate, and an extremely low 0.01% false
alarm rate. Since the false alarm rate is (approximately) independent of the interference power,
these filter settings would leave all “clean” weather virtually untouched, i.e., we would have a
very safe filter that is intended only to remove fairly strong interference. Such a filter could be
left running at all times without too much worry about side effects.
5–12
RVP8 User’s Manual
March 2006
Processing Algorithms
5.1.6 Large-Signal Linearization
The RVP8 is able to recover the signal power of targets that saturate the IF-Input A/D converter
by as much as 4–6 deciBels. This is possible because an overdriven IF waveform still spends
some of its time in the valid range of the converter, and thus, it is still possible to deduce
information about the signal.
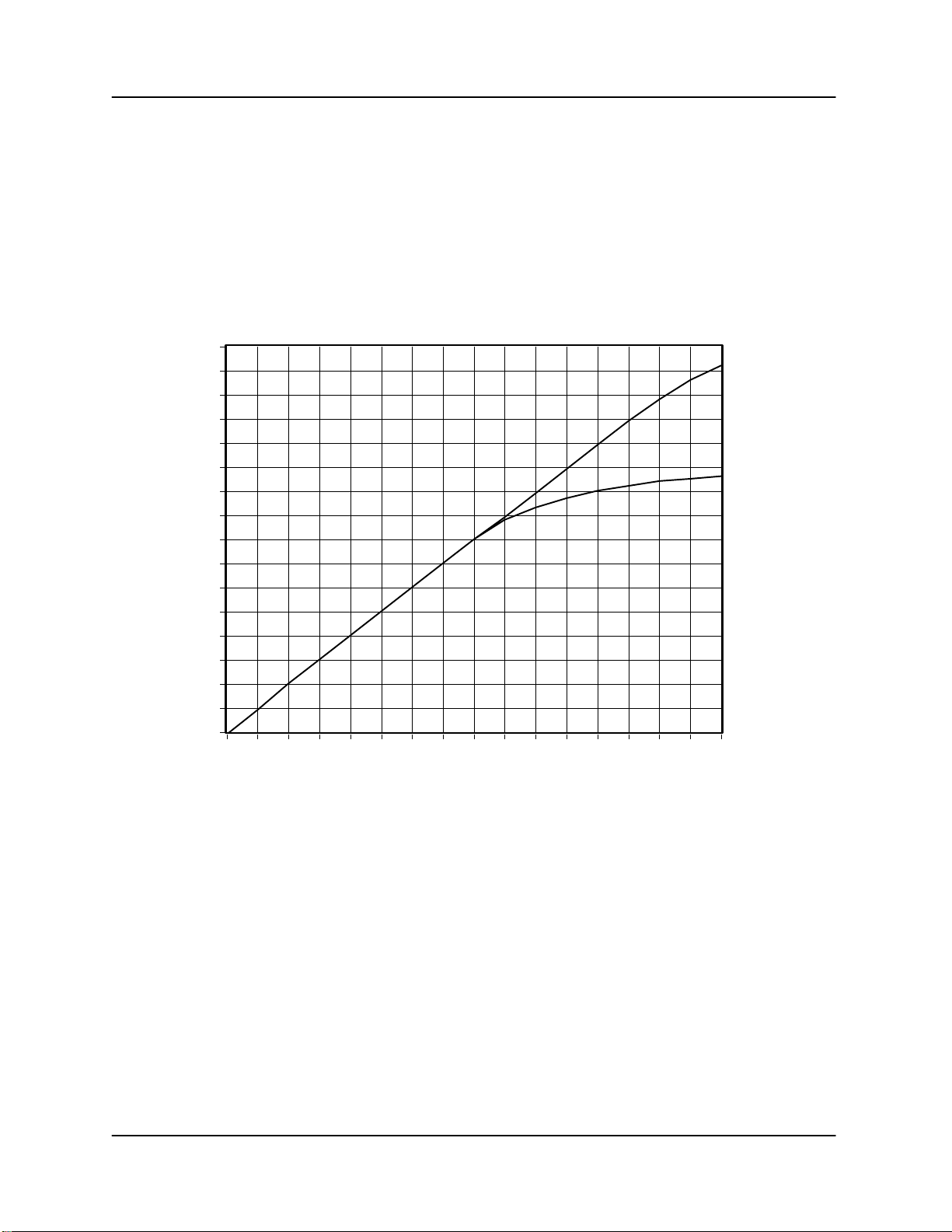
Figure 5–2 shows actual signal generator test measurements with normal A/D saturation (lower
line), and with the extrapolation algorithms turned on (upper line). The high-end linear range
begins to roll off at approximately +10dBm versus +5dBm, and thus has been extended by 5dB.
12
11
10
9
8
7
6
5
4
3
2
1
0
–1
–2
–3
–4
–4–3–2–10123456789101112
Figure 5–2: Linearization of Saturated Signals Above +4.5dBm (Rev B/C IFD)
The roll off starts at +4.5 dBm for the Rev. B&C IFD, and at +6 dBm for the Rev. D.
5.1.7 Correction for Tx Power Fluctuations
The RVP8 can perform pulse-to-pulse amplitude correction of the digital (I,Q) data stream based
on the amplitude of the Burst/COHO input. The technique computes a (real valued) correction
factor at each pulse by dividing the mean amplitude of the burst by the instantaneous amplitude
of the burst. The (I,Q) data for that pulse are then multiplied by this scale factor to obtain
corrected time series. The amplitude correction is applied after the Linearized Saturation
Headroom correction.
The mean burst amplitude is computed by an exponential average whose (1/e) time constant is
selected as a number of pulses (See Section 3.2.2). A short time constant will settle faster, but
will not be as thorough in removing amplitude variations (since the mean itself will be varying).
5–13

RVP8 User’s Manual
March 2006
Processing Algorithms
Longer time constants do a better job, but will require a second or two before valid data is
available when the transmitter is first turned on. The default value of 70 will give excellent
results in almost all cases.
Whenever the RVP8 enters a new internal processing mode (time series, FFT, PPP, etc.), the
burst power estimator is reinitialized from the level of the first pulse encountered, and an
additional pipeline delay is introduced to allow the estimator to completely settle. Thus, valid
corrected data are produced even when the RVP8 is alternating rapidly between different data
acquisition tasks, e.g., in a multi-function ASCOPE display. The additional pipeline delay will
not affect the high-speed performance when the RVP8 runs continuously in any single mode.
For amplitude correction to be applied, the instantaneous Burst/COHO signal level must exceed
the minimum valid burst power specified in the “Mb” setup section. If that level is not met, e.g.,
if the transmitter is turned off, then no correction is performed. Thus, the amplitude correction
feature conveniently “gets out of the way” when receiver-only tests are being performed.
The maximum correction that will ever be applied is
5dB. If the burst power in a given pulse
is more than 5dB above the mean, or less than 5dB below it, then the correction is clamped at
those limits. The power variation of a typical transmitter will easily be contained within this
interval (it is typically less than 0.3dB).
Instantaneous amplitude correction is a unique feature of the RVP8 digital receiver. Bench tests
with a signal generator reveal that an amplitude modulated waveform having 2.0dB of
pulse-to-pulse variation is reduced to less than 0.02dB RMS of (I,Q) variation after applying the
amplitude correction.
5–14

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2 Time Series (“I” and “Q”) Signal Processing
5.2.1 Time Series Processing Overview
This section describes the processing of the radar time series data (also called linear “video” or
“I” and “Q”) to obtain the meteorologically significant “moment” parameters: reflectivity, total
power, velocity, width, signal quality index, clutter power correction, and optional polarization
variables.
Recall that the time series synthesized by the FIR filter consist of an array of complex numbers:
where “j” is * 1
[
s
+
Im) jQ
m
1ń2
. The time series, are the starting point for all calculations performed
]
for m + 1, 2, 3, AAA, M
m
within the RVP8. There are several excellent references on the details of I and Q processing. The
reader is referred to Doviak and Zrnic’s text on the subject. The top part of Figure 5–3 shows I
and Q values for a simulated time series using the ascope utility.
There are two broad categories of time series signal processing:
S Time Domain Processing using the I and Q samples directly to calculate
“autocorrelations” and then using the autocorrelations to compute the moments. This is
used by many systems since the algorithms are very efficient requiring minimal storage
and computational power. However, time domain algorithms are generally not adaptive
or very flexible.
S Frequency Domain Processing using the I and Q samples to calculate a Doppler power
spectrum and then applying algorithms, such as clutter filtering or 2nd trip echo
filtering/extraction, in the frequency domain. The Doppler spectrum is then inverted to
obtain the autocorrelation functions and these are used to calculate the moments. The
frequency domain is well suited to more complex adaptive algorithms, i.e., where the
processing algorithm is optimized for the data.
The RVP8 supports the concept of “major modes” or processing modes to process the time
series. Currently the following major modes are supported by SIGMET:
S DFT/FFT Mode is a frequency domain approach which is used for most operational
processing applications. There are a variety of clutter filtering options, including the
GMAP algorithms (Gaussian Model Adaptive Processing).
S Pulse Pair Processing or PPP Mode is a time domain approach that is used primarily for
dual polarization applications.
S Random Phase Mode or RPHASE is a frequency domain approach similar to the
DFT/FFT, except that filtering and extraction of both the first and second trip echoes is
supported.
S Batch Mode during which a small batch of low PRF pulses is transmitted (e.g., for 0.1
degree of scanning) followed by a large batch of higher PRF pulses (e.g., for 0.9 degrees
of scanning) to determine which ranges are likely contaminated by second trip echo. This
5–15
RVP8 User’s Manual
March 2006
Processing Algorithms
was developed to support a US WSR88D legacy requirement. It is not supported in
SIGMET’s IRIS software.
The time and frequency domain approaches are described in the sections below.
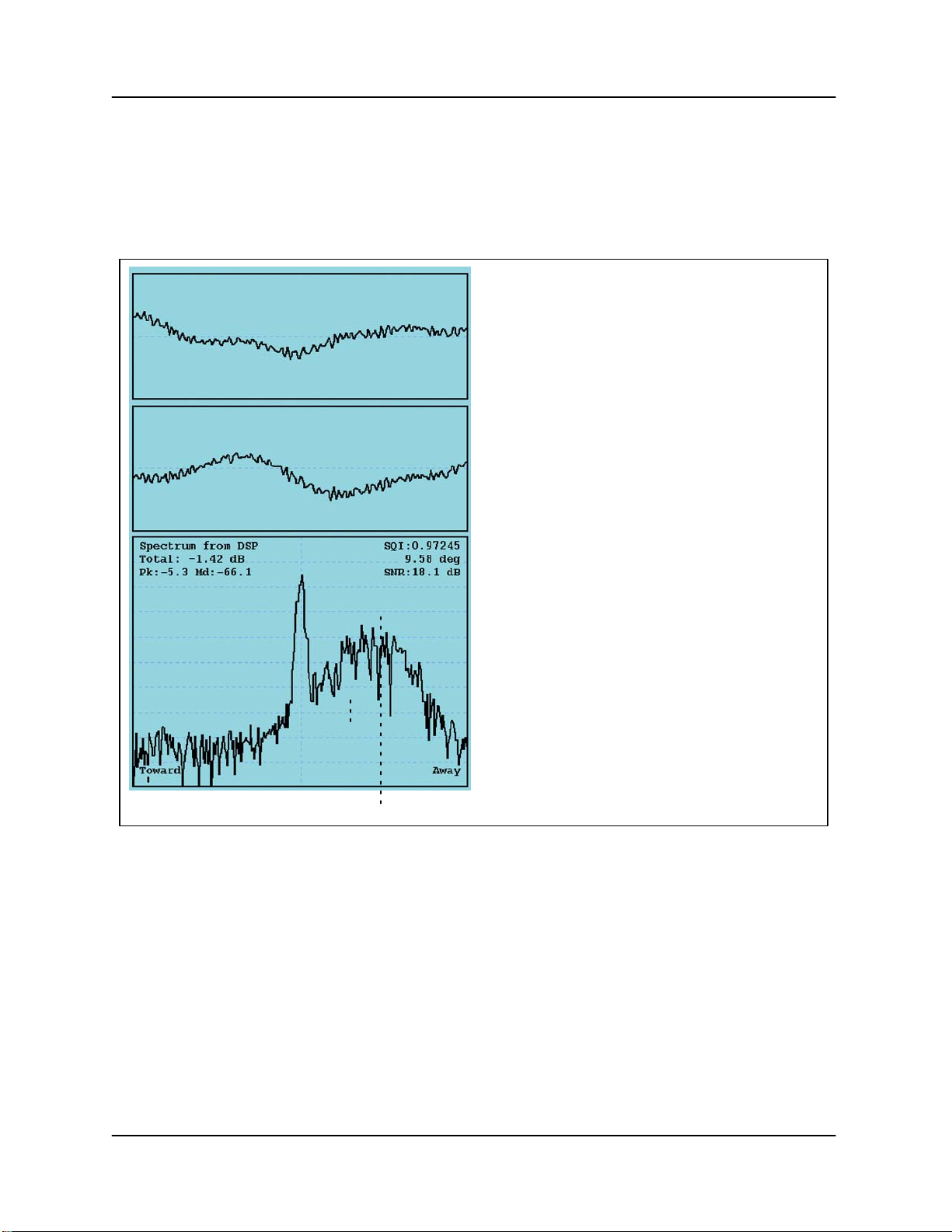
Figure 5–3: Example of time series and Doppler power spectrum
I
Q
Doppler
Spectrum
White Noise
Time
Ground Clutter
Weather Targets
Spectrum
Width
0
Velocity
σ
v
Mean Velocity
+VuĆVu
Time series of I and Q and the corresponding Doppler power spectrum obtained from the ascope utility using the
built-in simulator. The Doppler spectrum displays the radial velocity on the
X-axis over the unambiguous range or
“Nyquist” interval and the power in dB
AmplitudeAmplitude
relative to saturation on the y-axis.
Note that for illustration, this example
is based on 256 time series points (one
point per pulse) which yields 256 spectrum components. This is more than is
usually processed in actual operation.
The spectrum shows the three major
components of the Doppler spectrum:
Power
* White noise.
* Ground clutter at zero radial velocity .
* A spectrum of the weather targets
having a Gaussian shape characterized
by the weather power, mean velocity
and width (standard deviation), i.e., the
spectrum moments.
5–16

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.2 Frequency Domain Processing- Doppler Power Spectrum
The Doppler power spectrum, or simply the “Doppler spectrum”, is the easiest way to visualize
the meteorological information content of the time series. The bottom part of Figure 5–3 shows
an example of a Doppler power spectrum for the time series shown in the upper part of the
figure. The figure above shows the various components of the Doppler spectrum, i.e., typically
there is white noise, weather signal and ground clutter. Other types of targets such as sea clutter,
birds, insects, aircraft, surface traffic, second trip echo, etc. may also be present.
The “Doppler power spectrum” is obtained by taking the magnitude squared of the input time
series, i.e. for a continuous time series,
Ť
m+0
M
ȍ
2
wmsme
*j(2pńM)mk
2
Ť
S(w) + |F{s(t)}|
Here S denotes the power spectrum as a function of frequency ω, and F denotes the Fourier
transform of the continuous complex time series s(t). The Doppler power spectrum is
real-valued since it is the magnitude squared of the complex Fourier transform of s(t).
In practice a pulsed radar operates with discrete rather than continuous time series, i.e., there is
an I and Q value for each range bin for each pulse. In this case we use the discrete Fourier
transform or DFT to calculate the discrete power spectrum. Note that in the special case when
we have 2
algorithm (FFT), so called because it is significantly faster than the full DFT.
The DFT has the form:
Typically a weighting function or “window” wm is applied to the input time series sm to mitigate
the effect of the DFT assumption of periodic time series. The RVP8 supports different windows
such as the Hamming, Blackman, Von Han, Exact Blackman and of course the rectangular
window for which all spectral components are weighted equally. The typical form of a spectrum
n
input time series samples (e.g., 16, 32, 64, 128, ...), we use the fast Fourier transform
Sk+ |DFT
{
w
k
msm
2
}
|
+
5–17
RVP8 User’s Manual
March 2006
Processing Algorithms
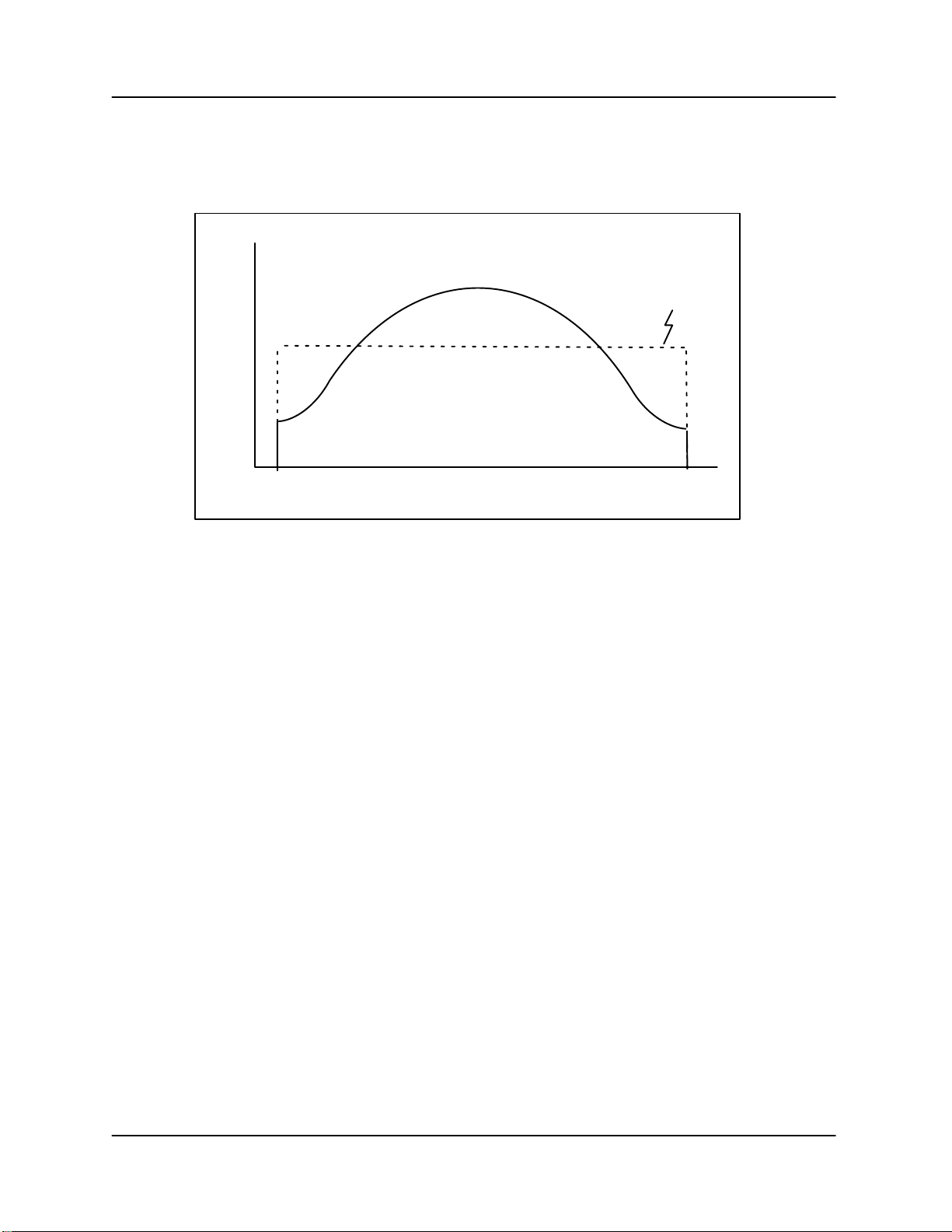
window is shown in the figure below which illustrates how the edge points of the time series are
de–emphasized and the center points are over emphasized. The dashed line would correspond to
the rectangular window. Note that the “gain” of the window is set to preserve the total power.
1
Weight
Time/Sample Index
Rectangular
M0
Figure 5–4: Typical form of a time series window
Even though the window gain can be adjusted to conserve the total power, there is an effective
reduction in the number of samples which increases the variance (or uncertainty) of the moment
estimates. For example the variance of the total power is greater when computed from a
spectrum with Blackman weighting as compared to using a rectangular window. This is because
there are effectively fewer samples because of the de-emphasis of the end points. This is a
negative side to using a window.
The DFT of the window itself is known as its impulse response which shows all of the
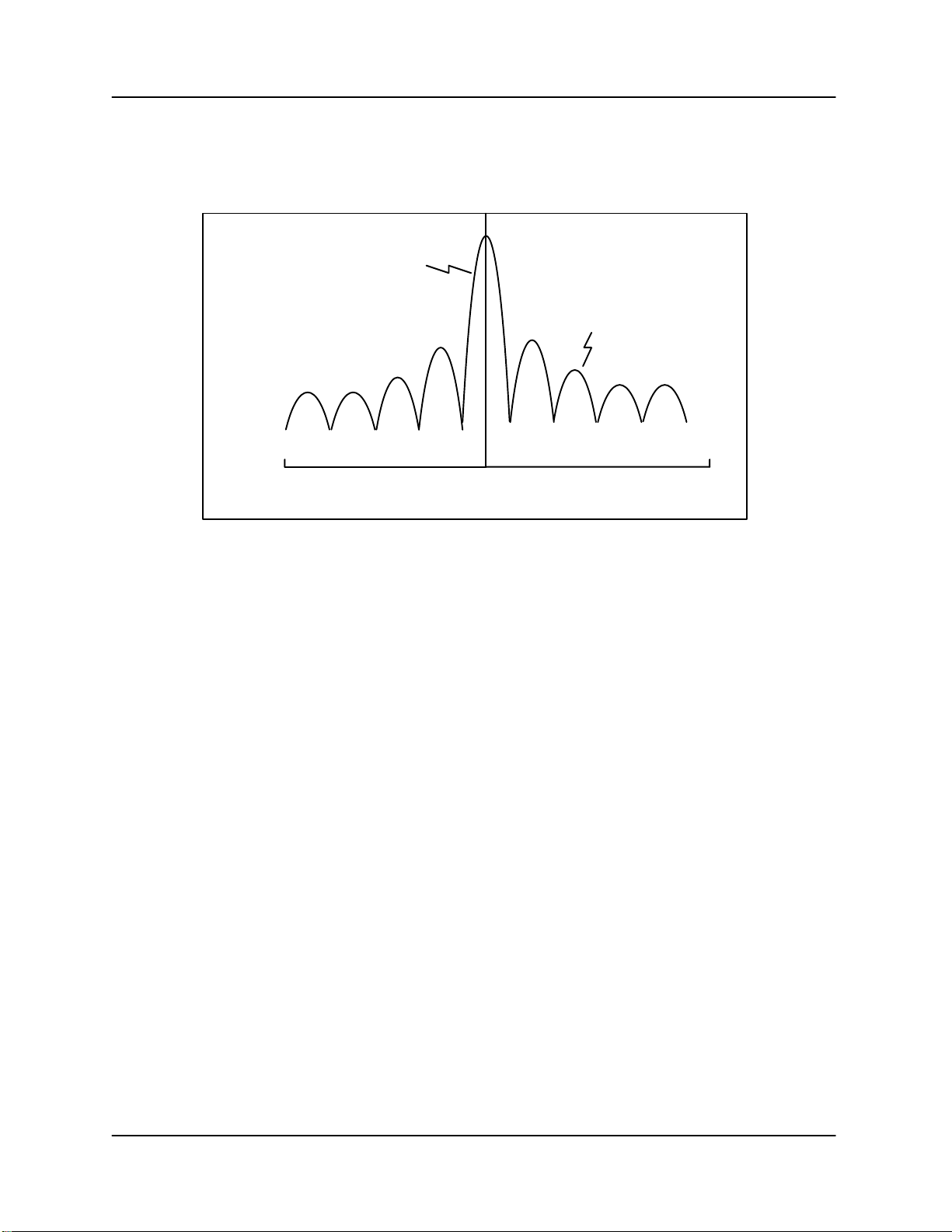
frequencies that are generated by the window itself. A generic example is shown in Figure 5–5
below which illustrates that these “side lobe” frequencies can have substantial power. This is not
a problem for weather signals alone, but if there is strong clutter mixed in, then the side lobe
power from the clutter can obscure the weaker weather signals. The rectangular window has the
worst sidelobes, but the narrowest window width. However, the rectangular window provides the
5–18
RVP8 User’s Manual
March 2006
Processing Algorithms
lowest variance estimates of the moment parameters (in the absence of clutter. More
“aggressive” windows have lower side lobe power at the expense of a broader impulse response
and an increased variance of the moment estimates.
Window Width
Side Lobes
Power
ĆM/2
Frequency
M/20
Figure 5–5: Impulse response of a typical window
So in summary of the DFT approach and spectrum windows:
S When the clutter is strong, an aggressive spectrum window is required to contain the
clutter power so that the side lobes of the window do not mask the weather targets. The
side lobe levels of some common windows are:
Rectangular 12 dB
Hamming 40 dB
Blackman 55 dB
S More aggressive windows typically have a wider impulse response. This effectively
increases the spectrum width. Rectangular is narrow, Hamming intermediate and
Blackman the widest.
S Windows effectively reduce the number of samples resulting in higher variance moment
estimates. Rectangular is the best case, Hamming is intermediate and Blackman provides
the highest variance moment estimates.
These facts suggest the best approach is to use the least aggressive window possible in order to
contain the clutter power that is actually present- i.e., an adaptive approach is the best.
5–19

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.3 Autocorrelations
The final spectrum moment calculation (for total power or SNR, mean velocity and spectrum
width) in all processing modes is based on autocorrelation moment estimation techniques.
Typically the first three lags are calculated, denoted as R
ways to calculate these, i.e., time domain or frequency domain calculation. In the PPP mode for
dual polarization, the autocorrelations are computed directly in the time domain while in the
DFT mode, they are computed by taking the inverse DFT the Doppler power spectrum in the
frequency domain. Note that only the first three terms need be calculated in the inverse DFT
case. The time domain and frequency domain techniques are nearly identical except that the
method of taking the inverse DFT of the power spectrum relies on the assumption that the time
series is periodic. Another difference is that for time domain calculation only a rectangular
weighting is used.
The time domain calculation of the autocorrelations and the corresponding physical models are:
Parameter and Definition Physical Model
M
1
T
+
o
R
+
o
R
+
1
R
+
2
ȍ
M
n+1
M
1
ȍ
M
n+1
1
M * 1
1
M * 2
sn* s
*
sȀ
sȀ
n
M*1
ȍ
n+1
M*2
ȍ
n+1
n
n
*
sȀ
sȀ
n
n)1
*
sȀ
sȀ
n
n)2
, R1 and R2. However, there are two
0
grgt(S ) C) ) N
grgtS ) N
grgtSe
grgtSe
j p VȀ*p2W2ń2
j 2p VȀ*2p2W
2
where M is the number of pulses in the time average. Here, sȀ denotes the clutter-filtered time
series,
g
s denotes the original unfiltered time series and the * denotes a complex conjugate. g
t
represent the transmitter and receiver gains, i.e., their product represents the total system gain.
r
and
Since the RVP8 is a linear receiver, there is a single gain number that relates the measured
autocorrelation magnitude to the absolute received power. However, since many of the
algorithms do not require absolute calibration of the power, the gain terms will be ignored in the
discussion of these. To for the unfiltered time series is proportional to the sum of the
R
meteorological signal S, the clutter power C and the noise power N.
is equal to the sum of
0
the meteorological signal S and noise power N which is measured directly on the RVP8 by
periodic noise sampling.
reflectivity factor which is a calibrated measurement. The physical models for
T
and R0 are used for calculating the dBZ values- the equivalent radar
o
R
, R1 and R
0
2
correspond to a Gaussian weather signal and white noise as shown in Figure 5–3. W is the
spectrum width and V’ the mean velocity, both for the normalized Nyquist interval on [–1 to 1].
The autocorrelation lags above and the corresponding physical models have five unknowns: N,
S, C, V’, W. Because the R1 and R2 lags are complex, this yields, effectively, five equations in
five unknowns using the constraint provided by the argument of R1. This closed system of
equations can be solved for the unknowns which is the basis for calculating the moments from
the autocorrelations.
5–20

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.4 Angle Synchronization
The exact value of M that is used for each time average will generally be the “Sample Size” that
is selected by the SOPRM command (See Section 6.3). However, when the RVP8 is in PPP
mode and antenna angle synchronization is enabled, the actual number of pulses used may be
limited by the number that fit within each ray’s angular limits at the current antenna scan rate.
The value of M will never be greater than the SOPRM Sample Size, but it may sometimes be
less. For example, at 1KHz PRF, 20_/sec scan rate, 1_ ray synchronization, and a Sample Size
of 80, there will be 50 pulses used for each ray (not 80). Note, however, that the number of
pulses used in the “batched” (non-PPP) modes will always be exactly equal to the Sample Size,
since those modes are allowed to use overlapping pulses.
5.2.5 Clutter Filtering Approaches
Each major mode implements clutter filtering as follows:
S DFT Mode uses frequency domain clutter filters.
S PPP Mode, used only for dual polarization. No clutter filtering is done in the PPP mode
since this will typically damage the polarization information.
S Random Phase Mode uses frequency domain clutter filters.
S Batch Mode uses a simple DC removal for the small batch clutter filter. The high PRF
large batch is then processed using the DFT mode.
In previous versions of SIGMET processors, an IIR (infinite implodes response) filter was
offered. The IIR filter, while requiring minimal storage and computation, has three major
drawbacks:
S The infinite impulse response requires a settling time when a transient occurs such as a
PRF change, or a spike clutter target. During the settling time, the transient response
degrades the performance of the filter.
S The filter is fixed width in the Nyquist interval. This means that it may be sufficiently
wide to remove moderate or weak clutter, but may not be wide enough to remove all of
the clutter when the clutter power is very strong and consequently wider in the Nyquist
interval. This causes operators to select wider filters than necessary so that strongest
clutter is adequately removed.
S The filter does significant damage to overlapped (zero velocity) weather signals, i.e.,
these will be significantly attenuated by the filter.
With the advent of the high speed processors such as the RVP8, there is sufficient storage and
computational power to implement frequency domain filters that, in some cases, are adaptive.
Because of the superiority of these filters, the legacy time domain IIR approach is no longer used
in the RVP8. The only mode that uses time domain filtering is the Batch mode for the low PRF
pulses (subtraction of the average I and Q to remove the DC component).
The various frequency domain filters available in the RVP8 are configured using the “mf” setup
command (Section 3.2.3). These are:
5–21

RVP8 User’s Manual
March 2006
S Type 0: Fixed width filters with interpolation
S Type 1:Variable width single slope adaptive processing
S Type 2: Gaussian model adaptive processing (GMAP)
These filters are described in in the sections detail below.
Processing Algorithms
5–22

RVP8 User’s Manual
March 2006
5.2.5.1 Fixed Width Clutter Filters
This filter, illustrated in Figure 5–6, removes a specified number of spectrum components
(5 in the example) and then interpolates across the gap using the minimum of a specified
number of “edge points” (2 in the example) to anchor the interpolation at each end of the gap.
This is a fairly simple legacy approach that uses interpolation to repair the damage caused
by the removal of components.
Figure 5–6: Example of fixed width
0
-20
-40
dB Power
-60
Processing Algorithms
Spectrum with ground clutter
0
-20
-40
dB Power
-60
0
-20
-40
dB Power
-60
0+Vu-Vu
Remove 5 interior points
Find minimum of 2 edge points
Interpolate across 5 center points
Velocity
This procedure attempts to preserve the noise level and/or overlapped weather targets. The result
is that more accurate estimates of dBZ are obtained. In extreme cases when the weather
spectrum is very narrow, there can still be some attenuation of weather of a broad filter is
selected.
5–23

RVP8 User’s Manual
March 2006
5.2.5.2 Variable Width Clutter Filter
This is similar in many ways to the fixed width filter except that the algorithm attempts to
extend the boundary of the clutter by determining which is the first component outside the
clutter region to increase in power. The filter is illustrated in the figure below.
Figure 5–7: Variable Width Clutter Filter
0
-20
-40
dB Power
-60
0
Processing Algorithms
Spectrum with ground clutter
-20
-40
dB Power
-60
0
-20
-40
dB Power
-60
0+Vu-Vu
Remove 3 interior points
Use slope to extend the clutter boundĆ
ary. Then find the minimum of the 2
edge points and interpolate.
Velocity
In the example above, the minimum number of points to reject is set to 3. The filter starts
at zero velocity and checks the slope to determine the point at which the power starts to increase. In the example, this results in the filter being extended by one point on the right. Note
that there is a selectable maximum number of points that the filter will “hunt”. The use of
the edge points for interpolation is identical to the fixed width case.
This filter allows users to specify a narrower nominal filter than the fixed width case and then
when the clutter is strong, this width is extended by the algorithm (the “hunt”). The interpolation attempts to preserve any overlapped clutter and weather.
5–24

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.5.3 Gaussian Model Adaptive Processing (GMAP)
GMAP is a new adaptive technique developed at SIGMET that is possible on a high-speed
processor such as the RVP8. GMAP has the following advantages as compared to fixed width
frequency domain filters or time domain filtering such as the IIR approach:
S The width adapts in the frequency domain to adjust for the effects of PRF, number of
samples and the absolute amplitude of the clutter power. This means that minimal
operator intervention is required to set the filter.
S If there is no clutter present, then GMAP does little or no filtering.
S GMAP repairs the damage to overlapped (near zero velocity) weather targets.
S The DFT window is determined automatically to be the least aggressive possible to
remove the clutter. This reduces the variance of the moment estimates.
The GMAP algorithm is described below.
GMAP Model Assumptions
GMAP makes several assumptions about the model for clutter, weather and noise, i.e.,
S The spectrum width of the weather signal is greater than that of the clutter. This is a
fundamental assumption required of all Doppler clutter filters.
S The Doppler spectrum consists of ground clutter, a single weather target and noise.
Bi-modal weather targets, aircraft or birds mixed with weather would violate this
assumption.
S The width of the clutter is approximately known. This is determined primarily by the
scan speed and to a lesser extent by the climatology of the local clutter targets. The
assumed width is used to determine how many interior clutter points are removed.
S The shape of the clutter is approximately Gaussian. This shape is used to calculate how
many interior clutter points are removed.
S The shape of the weather is approximately Gaussian. This shape is used to reconstruct
filtered points in overlapped weather.
GMAP Algorithm Steps
The steps used to implement the GMAP approach are shown schematically in Figure 5–8
and summarized below.
S Step 1: Window and DFT
First a Hamming window weighting function is applied to the IQ values and a discrete
Fourier transform (DFT) is then performed. This provides better spectrum resolution than
a fast Fourier Transform (FFT) which requires that the number of IQ values be a power
of 2. Note that if the requested number of samples is exactly a power of 2, then an FFT
is used.
5–25

RVP8 User’s Manual
March 2006
Power dB
Figure 5–8: GMAP Algorithm Steps
Step 1: Window and DFT
Apply window and DFT the input time series to obtain the Doppler
power spectrum. A Hamming window is used for the first trial.
Processing Algorithms
0
Vu–Vu
Step 2 (Optional): Dynamic noise power
If the noise level is not known, or if GMAP is recalculated using the
Blackman window for CSR>40 dB, then this step is performed. Re-organize the spectrum components in ascending order of intensity. The
theoretical relationship for noise is the curved line. The sum of the
power in the range 5% to 40% is calculated. This is used to determine
the noise level by comparing with the sum value corresponding to the
theoretical curve. Next, the power is summed beyond the 40% point
for both the actual and theoretical rank spectra. The point where the actual power sum exceeds the theoretical value by 2 dB determines the
boundary between the noise region and the signal/clutter region.
Power dB
Step 3: Remove clutter points
Use the total power of the three central spectrum points (indicated by the
three open circles) to fit a Gaussian having the selected nominal spectrum width in m/s (a function of the number of spectrum samples, PRF
and wavelength). The points within the intersection of the Gaussian clut-
Noise
ter and the noise level (the “Clutter Region”) are discarded (indicated by
Level
the dashed lines).
Clutter
Region
Power
Vu–Vu
Step 4: Replace clutter points
Dynamic Noise Case: Using the components which have been determined to be neither clutter nor noise (indicated by the filled circles), fit
a Gaussian and fill-in the clutter points that were removed in the previous
step (indicated by the open circles). Then re-fit the Gaussian with the replacement values inserted. Repeat the iteration until the computed power
does not change by more than 0.2dB AND the velocity does not change
Noise
by more than 0.5% of the Nyquist velocity.
Level
Fixed Noise Case: Similar except the spectrum points that are larger than
0
Vu–Vu
the noise level are used.
Signal/Clutter
Noise Region
Region
dB Power, I
0 100%
Percentage of spectrum points having power < I
Step 5: Recompute GMAP with optimal window
Determine if the optimal window was used based on the clutter-to-signal ratio (CSR)
IF CSR > 40 dB repeat GMAP using a Blackman window and dynamic noise calculation.
IF CSR > 20 dB repeat GMAP using a Blackman window. Then if CSR>25dB use Blackman results.
IF CSR < 2.5 dB repeat GMAP using a rectangular window . Then if CSR < 1 dB use rectangular re-
sults.
ELSE accept the Hamming window result.
5–26

RVP8 User’s Manual
March 2006
Processing Algorithms
S As mentioned in Section 5.2.2, when there is no or very little clutter, use of a rectangular
weighting function leads to the lowest-variance estimates of intensity, mean velocity and
spectrum width. When there is a very large amount of clutter, then the aggressive
Blackman window is required to reduce the “spill-over” of power from the clutter target
into the sidelobes of the impulse response function. The Hamming window is used as the
first guess. After the first pass GMAP analysis is complete, a decision is made to either
accept the Hamming results, or recalculate for either rectangular or Blackman depending
on the clutter-to-signal ratio (CSR) computed from the Hamming analysis. The
recalculated results are then checked to determine whether to use these or the original
Hamming result (see Figure 5–8 for details).
S Step 2: Determine the noise power
In general, the spectrum noise power is known from periodic noise power measurements.
Since the receiver is linear and requires no STC or AGC, the noise power is
well–behaved at all ranges. The only time that the spectrum noise power will differ from
the measured noise power is for very strong clutter targets. In this case, the clutter
contributes power to all frequencies, essentially increasing the spectrum noise level. This
occurs for two reasons: 1) In the presence of very strong clutter, even a small amount of
phase noise causes the spectrum noise level to increase, and 2) There is significant power
that occurs in the window side-lobes. For a Hamming window, the window side lobes are
down by 40 dB from the peak at zero velocity. Thus 50 dB clutter targets will have
spectrum noise that is dominated by the window sidelobes in the Hamming case. The
more aggressive Blackman window has approximately 55 dB window sidelobes at the
expense of having a wider impulse response and larger negative effect on the variance of
the estimates.
S When the noise power is not known, it is optionally computed using a dynamic approach
similar to that of Hildebrand and Sekhon (1974). The Doppler spectrum components are
first sorted in order of their power. As shown in Figure 5–8, the sorting places the
weakest component on the left and the strongest component on the right. The vertical
axis is the power of the component. The horizontal axis is the percentage of components
that have power less than the y-axis power value. Plotted on a dB scale, Poisson
distributed noise has a distinct shape, as shown by the curved line in Figure 5–8. This
shape shows a strong singularity at the left associated with taking the log of numbers near
zero, and a strong maximum at the right where there is always a finite probability that a
few components will have extremely large values.
S There are generally two regions: a noise region on the left (weaker power) and a
signal/clutter region on the right (stronger power). The noise level and the transition
between these two regions is determined by first summing the power in the range 5% to
40%. This sum is used to determine the noise level by comparing with the sum value
corresponding to the theoretical curve. Next, the power is summed beyond the 40% point
for both the actual and theoretical rank spectra. The point where the actual power sum
exceeds the theoretical value by 2 dB determines the boundary between the noise region
and the signal/clutter region.
5–27

RVP8 User’s Manual
March 2006
Processing Algorithms
S Finally there are two outputs from this step: a spectrum noise level and a list of
components that are either signal or clutter
S Step 3: Remove the clutter points
The inputs for this step are the Doppler power spectrum, the assumed clutter width in m/s
and the noise level, either known from noise measurement or optionally calculated from
the previous step. First the power in the three central spectrum components is summed
(DC ±1 component) and compared to the power that would be in the three central
components of a normalized Gaussian spectrum having the specified clutter width and
discretized in the identical manner. This serves as a basis for normalizing the power in
the Gaussian to the observed power. The Gaussian is extended down to the noise level
and all spectral components that fall within the Gaussian curve are removed. The power
in the components that are removed is the “clutter power”.
S A subtle point is the use of the three central points to do the power normalization of the
actual vs the idealized spectrum of clutter. This is more robust than using a single point
since for some realizations of clutter targets viewed with a scanning antenna, the DC
component is not necessarily the maximum. Averaging over the three central components
is a more robust way to characterize the clutter power.
S The very substantial algorithmic work that has been done thus far is to eliminate the
proper number of central points. The operator only has to specify a nominal clutter width
in m/s. This means that the operator does not need to consider the PRF, wavelength or
number of spectrum points- GMAP accounts for these automatically.
S A key point is that in the event that the sum of the three central components is less than
the corresponding noise power, then it is assumed that there is no clutter and all of the
moments are then calculated using a rectangular window. If the power in the three
central components is only slightly larger than the noise level, then the computed width
for clutter removal will be so narrow that only the central (DC) point shall be removed.
This is very important since, if there is no clutter then we want to do nothing or at worst
only remove the central component.
S Because of this behaviour, there is no need to do a clutter bypass map, i.e., turn-off the
clutter filter at specific ranges, azimuths and elevation for which the map declares that
there is no clutter. Because of the day-to-day variations in the clutter and the presence of
AP, the clutter map will often be incorrect. Since GMAP determines the no-filter case
automatically and then processes accordingly, a clutter map is not required.
S Step 4: Replace clutter points
The assumption of a Gaussian weather spectrum now comes into play to replace the
points that have been removed by the clutter filter. There are two cases depending on
how the noise level is determined under Step 2, i.e., the dynamic noise case and the fixed
noise level case.
S Dynamic noise level case: From Step 2, we know which spectrum components are
noise. From Step 3 we know which spectrum components are clutter. Presumably,
everything that is left is weather signal. An inverse DFT using only these components is
5–28

RVP8 User’s Manual
March 2006
Processing Algorithms
performed to obtain the autocorrelation at lags 0, 1. This is very computationally efficient
since there are typically few remaining points and only the first two lags need be
calculated. The pulse pair mean velocity and spectrum width are calculated using the
Gaussian model (e.g., see Doviak and Zrnic, 1993). Note that since the noise has already
been removed, there is no need to do a noise correction. The Gaussian model is then
applied using the calculated moments to determine a substitution value for each of the
spectrum components that were removed in Step 3.
S In the case of overlapped weather as shown in the Figure 5–8 example, the replacement
power is typically too small. For this reason, the algorithm recomputes R0 and R1 using
both the observed and the replacement points and computes new replacement points. This
procedure is done iteratively until the power difference between two successive iterations
is less than 0.2 dB and the velocity difference is less than 0.5% of the Nyquist interval.
S In summary of this step, the Gaussian weather model is used to repair the filter bias, i.e.,
the damage that is caused by removing the clutter points. An IIR filtering approach
makes no attempt to repair filter bias, rather the filter simply “digs a hole” into
overlapped weather.
S Step 5: Check for appropriate window and recalculate the moments if necessary.
The clutter power is known from the spectrum components that were removed in Step 3.
Since the weather spectrum moments and the noise are also known from Step 4, the CSR
can be calculated. The value of the CSR, is used to decide whether the Hamming
window is the most appropriate. The scenarios are described in Figure 5–8. The end
result is that very weak clutter is processed using a rectangular window, moderate clutter
a Hamming window, while severe clutter requires a Blackman window. Note that if no
clutter were removed in Step 3, then the spectrum is processed with a rectangular
window.
S The benefit of adaptive windowing is that the least aggressive window is used for the
calculation of the spectrum moments, resulting in the minimum variance of the moment
estimates.
GMAP Configuration
The ’mf’ command in the dspx TTY setups is used to configure GMAP filters. In the section
for the spectrum filters select filter “Type 2” and specify the width of the ground clutter in
m/s. This width is determined largely by your antenna rotation rate so you will want to configure several widths to deal with the different rotation rates in your operational scenario.
An example might be filters indexed 1-5 corresponding to widths from 0.1 to 0.5.
A good practice is to make a scan on a clear day while using ascope or other utility and observe what the actual width of the clutter is for your various scan rates. You will need to turnoff the clutter filtering to do this (pick “filter 0” for the all pass filter).
Example of Implementation
GMAP has undergone extensive evaluation for use in the US WSR88D ORDA network upgrade (Ice et al, 2004). They conclude that GMAP meets the ORDA requirements. Their
5–29

RVP8 User’s Manual
March 2006
study was based on a built-in simulator that is provided as part of the RVP8 and the ascope
utility. The simulator allows users to construct Doppler spectra, process them and evaluate
the results (Sirmans and Bumgarner, 1975). This is an essential tool for evaluating the system
performance.
Figure 5–9 shows an example of the simulations for the very difficult case when the weather
has zero velocity , i.e., it is perfectly overlapped with clutter. The upper left graph shows the
weather signal with –40 dB power without any clutter and without any GMAP filtering. The
graph at the upper right shows the same spectrum with 0 dB of clutter power added for a clutter width of 0.012 (0.3 m/s at S band, 1000 Hz PRF). This is a CSR of 40 dB. The panel at
the lower left shows the weather signal after GMAP filtering.
In each of the moment plots, there are several values that are displayed. The left-most number shows the value at the range cursor which is positioned as indicated by the vertical line.
To the right, the “m” value is the mean and the “s” value the standard deviation as averaged
over all range bins (1000 in this example). For velocity these are in normalized units expressed as a fraction of the Nyquist interval. For reflectivity the values are in dB.
Some key points are:
Processing Algorithms
S The mean velocity is correctly recovered as expected (the “m” value in the plot), but the
standard deviation is higher (0.06 vs 0.04 in normalized units).
S The “Cor dBZ” shows 40.2 dB of “C.Rej”. This is the difference between the “Tot dBZ”
and the “Cor dBZ” values. The expected value is 40 dB in this case. This indicates that
GMAP has recovered the weather signal in spite of the aggressive clutter filtering that is
required.
S The standard deviation of the “Tot dBZ” is greater in the weather plus clutter (4.35
normalized units) as compared to the weather-only case. This is caused by the
fluctuations in the clutter power in the Gaussian clutter model.
S The standard deviation of the Cor dBZ after GMAP filtering, while not as low as for the
weather-only case are lower than the weather plus clutter case. In other words, the
GMAP processing removes some of the high variance in the dBZ estimates that is caused
by clutter, but is not quite as good as doing nothing.
5–30

RVP8 User’s Manual
March 2006
Processing Algorithms
Figure 5–9: GMAP example
Weather only Weather plus clutter
Simulation Characteristics
Clutter Weather Units
Power 0 –40 dB
Vel 0 0 Any
Width 0.012 0.1 Normalized
PRF 1000 Hz Window Blackman
ModeFFT Samples 64
“Mag Spec”: Doppler Spectrum in dB Units spanning
the Nyquist interval.
“Velocity”: Mean velocity of the spectrum in over Nyquist interval. Mean “m” and standard deviation values
“s” are for the normalized interval ±1.
“Tot dBZ”: Power in dB of weather and clutter. Mean
“m” and standard deviation values “s” are in dB.
“Cor dBZ”: Power in dB after GMAP filtering. Mean
“m” and standard deviation values “s” are in dB.
“<m: ...s: ...>” mean and standard deviation over all
ranges, in this case 1000 range bins.
5–31

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.6 Range averaging and Clutter Microsuppression
The next step (optional) is to perform range averaging. Range averaging can be performed over
T
2, 3, ..., 16 bins. This is accomplished by simply averaging the
reduces the number of bins in the final output to save processing both in the RVP8 and in the
host computer.
At the user’s option, the range averaged data can be restricted to include only those bins which
have an estimated clutter-to-signal ratio that falls within the CCOR threshold interval. By
excluding isolated point clutter targets from the range average the sub-clutter visibility of the
averaged data is increased. Specifically, the Doppler test that is applied to each bin in order that
it contribute to the overall sum is:
, R0, R1 and R2 values. This
0
10logR0* 10 log T0u CCOR
thresh
.
5.2.7 Reflectivity
The corrected reflectivity Z is output using a log scale based on the following equation:
T0* N
dBZ + 10 log
ƪ
This equation is simply a dB version of the familiar radar equation for distributed targets. The
relationship between the measured autocorrelation function, the received signal and the noise can
be expressed as:
where gt and gr represent the transmitter and receiver gains, S is the average back scattered
power from the targets and N is the measured average noise power. Neglecting attenuation and
the contribution of ground clutter (for the moment), the radar equation can be written as.
Z + CSr
ƫ
) dBZo) 20 log r ) ar ) CCOR
N
To+ gtgrS ) N
2
Cr
N
2
+ ƪ
0
ƫ
rgt
g
2
To* N
r
ƪ
ƪ
ƫ
2
r
o
ƫ
N
where C is the radar constant and ro is a reference range which we will later set to 1 km. This is
identical to the first three terms of the dB version of the equation with the definition that:
2
Cr
+
o
+ Cr
rgt
g
Z
o
2
Iowhere I
o
N
N
+
o
rgt
g
Zo is called the calibration reflectivity factor. It is the equivalent radar reflectivity factor at the
reference range when the return signal power is equal to the noise power (SNR=0 dB). It is
sometimes called the minimum detectable dBZ at 1 km, though it is more correct to call it the
0dB SNR detection level (See Figure 5–10). The parameter I
is the measured noise power at IF
o
with appropriate calibration for the system gain. Calibration of the RVP8 involves defining the
radar constant C and measuring the value of I
. This is discussed in detail in Section 5.4.
o
5–32

RVP8 User’s Manual
March 2006
Essentially, the measurement of Io is based on the measurement of the system noise at the time
of calibration. However, if the receiver gain were to change after calibration, the use of periodic
noise sampling properly corrects for this. For example, if the receiver gain were to change by a
factor k, then we would measure a noise value of kN and an autocorrelation value of kT
2
Cr
N
Z + CSr
Thus the k’s cancel to give us the same result for Z. This makes the approach robust to system
gain fluctuations. Another way of saying this is that as long as the system sensitivity (noise
figure) does not change, then the system does not require re-calibration.
The individual terms in the dB form of the equation are summarized below.
T0* N
ƪ
1st Term :
The effect of this term is to subtract the measured noise and then divide by that noise. The
result is a Signal-to-Noise ratio.
10log
N
2
+ ƪ
ƫ
: Signal to Noise Ratio
0
rgt
g
2
kTo* kN
r
ƪ
ƫƪ
ƫ
2
r
o
kN
ƫ
Processing Algorithms
, i.e.,
o
dBZ
2rd Term:
dBZ
is the minimum detectable dBZ at a reference range ro=1 km,
o
3th Term:
This term is the
4th Term:
This term accounts for gaseous attenuation. The constant a is set in the RVP8 EEROM since
it is a function of wavelength. For a C-band system the default value is 0.016 dB per km (for
two-way path attenuation).
5th Term: CCOR: Clutter Correction
This term corrects for the measured ground clutter. It’s derivation is discussed in section
5.2.11.
: Calibration Reflectivity (see discussion above)
o
20logr : Range Normalization
2
r
ƪ
ƫ
range normalization expressed in dB form.
r
o
ar : Gaseous Attenuation Correction
5–33

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.8 Velocity
For a Doppler power spectrum that is symmetric about its mean velocity, the velocity is obtained
directly from the argument of the autocorrelation at the first lag, i.e.,
l
q
where q
4pt
+" p , then V +" V
1
s
+
l
4t
V
u
+ argNJR
1
where the unambiguous velocity is ,
u
.
s
l is the radar wavelength, t
interval
[
* p, p
]
. When q
V +
is the sampling time (1/PRF). q1 is constrained to be on the
s
1
If the absolute value of the true velocity of the scatterers is greater than
calculated by the RVP8 is folded into the interval
ƪ
* V
u
, V
ƫ
u
Nj
.
1
V
, then the velocity
u
, which is called the Nyquist
interval. Folding is usually easily recognized on a color display by a discontinuous jump in
velocities. For example, if the true velocity is
RVP8 is
* Vu) DV, which is 2V
away from the true mean velocity.
u
Vu) DV, then the velocity calculated by the
For 8-bit outputs, rather than calculating the absolute velocity in scientific units, the RVP8
calculates the mean velocity for the normalized Nyquist interval [–1,1], i.e., the output values
are,
q
VȀ+
For example, an output value of –0.5 corresponds to a mean velocity of
normalized velocity
VȀ is more efficient use of the limited number of bits.
1
.
p
* Vuń2. The
5.2.9 Spectrum Width Algorithms
The spectrum width is a measure of the combined effects of shear and turbulence. To a lesser
extent, the antenna rotation rate can also effect the spectrum width. At high elevation angles, the
fall speed dispersion of the scatterers also effects spectrum width.
There are two choices for the spectrum width algorithm used in the RVP8, depending on the
speed and accuracy that are required for the application:
R0,R
“fast” algorithm valid when SNR >> 10 dB
1
R0,R1, R
“accurate” algorithm for SNR >> 0 to 5 dB
2
The approach used is selected in the SOPRM command. The two appr oaches are described below:
R0,R
Width Algorithm
1
Given samples of the Doppler autocorrelation function, numerous estimates of spectral variance can be computed (Passarelli & Siggia, 1983). The particular estimator used by the
RVP8 employs the magnitudes of
R
and R1 and assumes that the Doppler spectrum is
0
Gaussian (usually an acceptable assumption) and that the signal-to-noise ratio is large. Specifically we have (similar to Srivastava, et al 1979):
R
Variance + 2ln
ƪ
| R1|
o
ƫ
+*2ln[SQI
]
5–34

RVP8 User’s Manual
March 2006
where “ln” represents the natural logarithm. This can be compared to the expression in the
preceding section for SQI to illustrate that this expression for the variance is only valid when:
Processing Algorithms
SNR
SNR ) 1
[ 1
which occurs when the SNR is large.
This variance estimator is normalized to the Nyquist interval in units of
2
p
example, a variance of
ń25 would be obtained from a Gaussian spectrum having a stan-
[
* p, p
]
. Thus, for
dard deviation equal to one fifth of the total width of the plotted spectral distribution. For
scientific purposes, the spectrum width (standard deviation) is more physically meaningful
than the variance, since it scales linearly with the severity of wind shear and turbulence. For
these reasons, the width W is output by the RVP8:
Ǹ
W +
Variance
p
Again, for efficient packing in 8-bits, width is normalized to the Nyquist interval [–1, 1 ].
For the example given above, the output width W would be (1/5). To obtain the width in meters per second, one multiplies the output width by
R0,R1,R
Width Algorithm
2
The width algorithm in this case is similar except that the addition of
V
.
u
R
extends the validity
2
of the width estimates to weak signals. In this case the variance is:
| R1|
2
ƪ
Variance +
ln
3
| R
ƫ
|
2
The output width W is then defined as in the previous section.
5.2.10 Signal Quality Index (SQI threshold)
An important feature of the RVP8 is its ability to eliminate signals which are either too weak to
be useful, or which have widths too large to justify further analysis. This is done via the signal
quality index (SQI) which is defined as:
| R
|
SQI +
The SQI is the normalized magnitude of the autocorrelation at lag 1 and varies between 0 for an
uncorrelated signal (white noise) to 1 for a noise-free zero-width signal (pure tone). Mean
velocity estimates are degraded when the spectrum, width is large or when the signal-to-noise
ratio is weak. The SQI is a good measure of the uncertainty in the velocity estimates and is a
convenient screening parameter to compute. In terms of the Gaussian model, the SQI is :
SQI +
SNR
SNR ) 1
where the SNR is the signal-to-noise ratio. For very large SNR’s the SQI is a function of the
spectrum width only. For a zero-width pure tone (W=0), the SQI is a function of the SNR only
(e.g., for W=0, an SNR of 1 corresponds to SQI=0.5). The SQI threshold is typically set to a
value of 0.4 to 0.5.
1
R
0
2
*p2W
2
e
5–35

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.11 Clutter Correction (CCOR threshold)
In addition to calculating the R0, R1 and optional R2 autocorrelation terms, which are based on
T
filtered time series data, the RVP8 also computes
comparing the total filtered and unfiltered powers at each range bin, a clutter power, and hence a
clutter correction, for that bin can be derived. The clutter correction is defined as,
which is the total unfiltered power. By
0
CCOR + 10 log
S
C ) S
+ 10 log
1
CSR ) 1
where S is the weather signal power, C is the clutter power and CSR is the clutter-to-signal
R
ratio. The algorithm for calculating CCOR depends on whether the optional
autocorrelation
2
lag is computed as described below.
R0,R
Clutter Correction
1
In this case CCOR is estimated from,
R
0
ƪ
ƫ
T
0
1 )
CSR ) 1 )
1
SNR
1
SNR
ƫ
+ 10log
CCOR
S ) N
ƪ
C ) S ) N
+ 10log
est
ƫ
+ 10 logƪ
Here, the expression is strictly valid only when the signal-to-noise ratio (SNR=S/N) is large.
Thus when the 2-lag approach is used, the clutter corrections are not as accurate for weak
weather signals. However, the error is typically less than 3 dB.
R0,R1,R
Clutter Correction
2
In this case there is enough information to compute the clutter signal and noise power independently. The algorithm for CCOR is:
CCOR
+ 10 log
est
S
C ) S
+ 10 log
1
CSR ) 1
The clutter power is computed from:
C + To* R
ƪ
+
o
C ) S ) N
ƫ*ƪ
S ) N
ƫ
The signal power S is then computed from:
2
p2W
S + | R1|exp
2
W is the width that has been previously calculated. This approach yields more accurate results for the clutter correction in the case of a low SNR.
5–36

RVP8 User’s Manual
March 2006
Processing Algorithms
5.2.12 Weather Signal Power (SIG threshold)
A parameter called SIG is also calculated to provide an estimate of the weather signal-to-noise
ratio in dB for thresholding. The SIG calculation is different depending on the whether the
R
optional
autocorrelation is computed.
2
R0,R
In this case the SIG is computed as follows:
This term represents the SNR after the removal of clutter. The CCOR value is the one described for
R0,R1,R
In this case the SIG is computed based on the SNR which is:
where the signal power S is determined as described in the preceding section.
Calculation
1
R0,R
1
Calculation
2
SIG + 10 log
in the previous section.
SIG + 10 log
ƪ
T0* N
N
ƪ
R
ƫ
2pS
* 2pS
0
) CCOR
ƫ
5.2.13 (Signal+Noise)/Noise Ratio (LOG threshold)
A threshold parameter called LOG is also calculated to provide a signal strength estimate that is
useful for qualifying reflectivity. For historical reasons, the LOG threshold is not the true SNR
(whose dB representation can be both positive and negative) but rather, the ratio of Signal plus
Noise to Noise, which always has a positive representation in dB. Specifically:
LOG + 10 log
LOG + 10 log
T
0
ƪ
ƫ
(when applied to the dBT parameter)
N
R
0
ƪ
ƫ
(when applied to all other parameters)
N
5–37

RVP8 User’s Manual
March 2006
Processing Algorithms
5.3 Thresholding
An important feature of the RVP8 is its ability to accept or reject incoming data based on derived
properties of the signals themselves. Typically, “rejected” data are not displayed by the user’s
software, thus making for very clean weather presentations.
5.3.1 Threshold Qualifiers
For data quality control, each RVP8 output parameter can be qualified, i.e., either accepted or
rejected for output, based on four threshold criteria:
ID Criterion Name Pass Criterion
LOG
SQI
CCOR
SIG
(Signal+Noise)-to-Noise Ratio LOG > threshold
Signal Quality Index SQI > threshold
Clutter Correction CCOR > threshold
Weather Signal Power SIG > threshold
The calculation of the measured levels (e.g., SQI) for each of these qualifications has been
described in previous sections of this chapter. All four qualification criteria can be switched on
and off independently, and the threshold levels (e.g.,
SQI
) can each be set independently.
thresh
Further, each qualifier test can be AND’d and OR’d with any other. This allows very complex
thresholds criteria to be constructed as required. The four threshold qualifiers are summarized
below.
LOG This is a measure of signal strength that is usually used for the thresholding of
reflectivity data. The default LOG threshold value is 0.5 dB.
SQI The SQI threshold is typically used for velocity and width thresholding since it is a
measure of the coherency. It is a number between 0 and 1 (dimensionless) where 0 is
perfect white noise and 1 is a pure tone (perfect Doppler signal). The default SQI
threshold value is 0.5.
CCOR The clutter correction threshold is typically used to reject measurements when the
clutter in a range bin is very strong (i.e., when the calculated CCOR is a large
negative number in dB). The appropriate value depends on the coherency of the radar
system. The default threshold is set to –25 dB. Threshold values less than this (more
negative) reject fewer clutter bins. Threshold values closer to zero reject more clutter
bins.
SIG This is typically used only for thresholding the spectrum width to assure that the
signal power is strong enough for an accurate width measurement. The default
R
threshold value is 10 dB. If
processing is used, this can usually be reduced to 5 dB
2
for width thresholding.
The following are the default threshold combinations for each of the parameters that can be
selected for output from the RVP8:
5–38

RVP8 User’s Manual
March 2006
Processing Algorithms
Parameter Description Threshold
dBZ Reflectivity with clutter correction LOG and CCOR
dBT Reflectivity without clutter correction LOG
V Mean velocity SQI and CCOR
W Spectrum width SQI and CCOR and SIG
ZDR Differential reflectivity LOG
5.3.2 Adjusting Threshold Qualifiers
The effect of the various threshold qualifiers for each output parameter are discussed in this
section. In optimizing thresholds for your application, it is recommended that you change only
one parameter (level or criterion) at a time so that you can verify the effect. Some hints for
optimizing the levels for the default criteria are provided below:
LOG To optimize the LOG level, display dBT or dBZ and select the lowest value of the
threshold that eliminates the display noise. If the LOG level is set too high you lose
sensitivity. Note that if you average more pulses or ranges, then the threshold level
can usually be reduced.
SQI To optimize the SQI level, display velocity and select the lowest value of the
threshold that eliminates the display noise. If the SQI level is set too high you lose
sensitivity. In general, you should see a greater area covered by velocity than
reflectivity since the velocity is more sensitive. If you do not, you should reduce your
SQI threshold. Note that if you average more pulses or ranges, then the threshold
level can usually be reduced.
CCOR This is used to eliminate clutter targets that are very strong. It should not be set to
eliminate all clutter targets on a clear day since this means that you are losing
sensitivity. To optimize the CCOR threshold it is best to know your system coherency
in terms of dB of clutter cancelation. Start at a value of 10 dB greater (closer to 0)
than this. Now display a PPI of dBZ at an antenna elevation of ~1 degree. The
display should be relatively clean of any clutter targets since most will be rejected.
Now reduce the CCOR (more negative) to increase the number of clutter targets on
the display until the number of clutter targets does not increase. The optimum value
of the CCOR is approximately 5 dB more (closer to zero) than this point. For
example, if the number of clutter targets is a maximum at –35 dB, then set the CCOR
to ~–30 dB. Note that your clutter filter selection will effect the result.
SIG This should be done last. To optimize the SIG level, display the width W and select
the lowest value of the threshold that eliminates the display noise. If the SIG level is
set too high you lose sensitivity. Note that if you average more pulses or ranges, then
the threshold level can usually be reduced.
When thresholding dBZ and dBT reflectivity data with SQI, the comparison value for accepting
those data is the secondary SQI threshold that is defined via a slope and offset from the primary
user value (see Mf command). This secondary threshold is more permissive (lower valued), and
5–39

RVP8 User’s Manual
March 2006
Processing Algorithms
is traditionally used to qualify LOG data only in the Random Phase processing mode. But the
secondary SQI threshold is applied uniformly in all processing modes whenever reflectivity data
are specified as being thresholded by SQI.
This gives you more freedom in applying an SQI threshold to your LOG data, because the cutoff
value for reflectivity can be chosen independently from the cutoff value for the other Doppler
parameters. The full SQI test would not normally be applied to LOG data because of the
so-called “black hole” problem, i.e., loss of LOG data within regions of high shear, even though
the reflectivity itself was strong. You may experiment with applying a secondary SQI threshold
to help cleanup the LOG data, but without introducing any significant black holes.
5.3.3 Speckle Filters
A speckle filter is a final pass over each output ray, wherein isolated bins are removed. There are
two speckle removers in the RVP8.
S 1D single-ray speckle filter. This can be used for any output parameter.
S 2D 3x3 speckle filter. If enabled, this is applied only to T, V, Z and W.
The 1D speckle filter is the default technique. The 2D 3x3 filter is enabled by selection in the
mp TTY setups:
2D Final Speckle/Unfold “User” or “Always”
Both of these speckle filters remove isolated data points that are likely to be noise, interference,
aircraft, birds or other point targets. Meteorological targets typically occupy multiple range bins
so are not effected by the speckle filter. There are two primary benefits derived from using a
speckle filter:
S Displays look “cleaner” to observers.
S Thresholds can be set slightly more sensitive without increasing the number of noise
pixels.
The 2D 3x3 filter actually performs data filling of “missing speckles” as well as eliminating
isolated speckle bins. The two algorithms are discussed below.
1D Speckle Filter
A ray is the basic azimuth unit of the RVP8 (e.g., 1 degree) over which the samples are averaged
to obtain the output base data (T, Z, V, W). For this filter, a speckle is defined as any single,
valid bin (not thresholded), having thresholded bins on either side of it in range. Any such
isolated bin in a ray is set to “threshold”. The algorithm is shown schematically below.
Note that there are two independent 1D speckle removers– one for the reflectivity data (dBT,
dBZ and ZDR) and one for the Doppler data (V and W). Each one should be switched on or off,
depending on the specific nature of the targets being observed. For example, when making a
clutter map of the area, one would certainly want to switch both speckle filters off.
5–40

RVP8 User’s Manual
Â
March 2006
Processing Algorithms
1D Speckle Filtering
Input Ray
Output Ray
Â
Range
XX
Indicates Thresholded Bin
Indicates Valid Bin
X Indicates Speckle
2D 3x3 Speckle Filter
The 2D filter examines three adjacent range bins from three successive rays in order to assign a
value to the center point. Thus, for each output point, its eight neighboring bins in range and
time are available to the filter. Only the dBZ, dBT, Vel , and Width data are candidates for this
filtering step; all other parameters are processed using the default 1D speckle filter.
The rules for the filter are as follows:
Center Point Action
Assign Threshold Else
Valid Center Point If there are no or only one
other valid point in the 3x3.
Thresholded Center Point If there are 5 or fewer valid
neighbors in the 3x3.
Do Nothing. Pass the center
point value as-is.
If there are 6 or more valid
neighbors in the 3x3, average
to fill the center point.
Thus the 2D 3x3 filter performs 2 functions:
S Filling by interpolation.
S Thresholding of isolated noise bins.
Some examples are shown graphically in the figure below.
For dBZ, dBT, and Width, the interpolated value for filling is computed as the arithmetic
average of all available neighbors. For Vel , it is not possible to define a meaningful average in a
simple way; so the nearest valid neighbor is simply filled in.
The filter has some interesting properties when combined with other algorithms.
Dual PRF Unfolding
Dual–PRF velocity unfolding is computed within the 3x3 filter whenever both are enabled.
There are two steps to the process:
S Step 1: The most recent and the previous ray are used. For every valid point in the most
recent ray, the algorithm performs a search among the three nearest neighbors in the
previous ray to find a valid velocity. The search pattern is shown at the bottom of the
previous figure. This larger selection of alternate–PRF bins makes it more likely that the
algorithm will find the pairs of Low/High PRF data that are required for unfolding.
5–41

RVP8 User’s Manual
ÂÂÂ
Â
Â
Â
March 2006
Threshold if center point is valid but there are no or only one valid neighbor.
Azimuth
Fill thresholded center point with average if there 6 or more valid neighbors.
-1
1
0
Range
2D 3x3 Filtering Concepts
Z
Z
Z
0
00
0*1
output
00
1-1
+ Threshold
Â
Processing Algorithms
Azimuth
-1
Z
Z
*11
*1*1
1
0
Z
01
Z
0*1
0
Z
11
Z
10
ÂÂ
1-1
Range
2D Velocity Unfolding Step 1: Search pattern for valid second velocity
V2
Azimuth
-1
0
V1
1*1
3
1
Â
0
00
2
ÂÂ
1-1
PRF2
PRF1
Range
Indicates Thresholded Bin
Z
output
00
+
*11
6
*1*1)Z0*1
[
) Z01) Z11) Z10) Z
Z
S Step 2: The unfolded velocities are then subjected to the standard 3x3 filtering.
]
Dual PRF, Random Phase Processing
In random phase processing, the “seam” at the start of the second trip is always problematic
since the transmitter main bang and nearby clutter will virtually always wipe out the first few
2nd trip range bins. At a constant PRF the 2nd trip seam is always at the same range, but in
dual PRF random phase mode, the seam is different each ray. Thus thresholded bins at the
seam of the high PRF can be surrounded on either side by valid bins taken at the low PRF.
The 3x3 filter has the effect of interpolating the reflectivity and width data over the bins at
the 2nd trip seam. Velocity data will also be filled–in using the nearest neighbor. Thus the
5–42

RVP8 User’s Manual
March 2006
2D filter mitigates much of the damage that is caused at the 2nd trip seam to make a nearly
seamless display.
Processing Algorithms
5–43

RVP8 User’s Manual
March 2006
Processing Algorithms
5.4 Reflectivity Calibration
The calculation of reflectivity described in Section 5.2.7 required the calibration reflectivity
dBZ
. This section describes it’s derivation. You can use the zauto utility to perform the
o
calibration. (See the IRIS/RDA Utilities Manual.)
Figure 5–10 Model Intensity Curve
)
o
10Log(I
–5dB SNR
Min Detectable
1.2dB Detection
Threshold (LOG)
10Log(N)
RVP8 Measured Power (2dB per Major Div)
Power at Antenna Feed (2dB per Major Division)
5.4.1 Plot Method for Calibration of
This approach generates the curve shown above (red) which determines the value of Io. The
general procedure is to connect a calibrated signal generator to the radar receiver and inject
known power levels to generate a calibration plot of measured power vs the inserted power at the
antenna feed, similar to that in Figure 5–10. The calibration reflectivity
the radar constant and the value of I
the Noise level.
Why does this geometric construction yield the value of I
of the RF and IF components leading up to the RVP8. The green line can be interpreted as the
response of an ideal noise-free amplifier having gain G
the real-world amplifier(s) whose equivalent front-end noise is I
, which is the intercept of the straight line fit (green) with
o
I
o
dBZ
is computed from
o
? Let GdB represent the overall gain
o
, while the red curve is the response of
dB
:
o
(Red) 10 log10( P
(Green) 10 log
10
( P
) + GdB) 10 log10( PIN) Io)
OUT
) + GdB) 10 log10( PIN)
OUT
5–44

RVP8 User’s Manual
March 2006
Processing Algorithms
The measured receiver noise is the horizontal asymptote of the red curve, i.e., the value of the
red curve when the input power P
is zero:
IN
10log10( N ) + GdB) 10 log10( Io) .
Intersecting this measured noise level with the green straight line gives:
GdB) 10 log10( Io) + GdB) 10 log10( PIN)
From which we see that the input power at the point of intersection is, indeed, Io .
Note that I
noise power. This should not be confused with the minimum detectable power P
is the received signal level that will produce 0dB SNR, i.e., signal power equal to
o
which
MDS
typically will be several dB lower, depending on processor settings. In the above example, a
1.2dB LOG detection threshold is shown (horizontal blue line) for the received signal. If the
RVP8 is applying sufficient range and time averaging so that thermal noise alone produces very
few false alarms above 1.2dB, then P
will be a full 5dB lower than Io. We would expect a
MDS
detection rate of roughly 50% for echoes arriving at this “minimum detectable” level.
Typically a CW test signal is used to generate the test curve shown in Figure 5–10. Follow the
instructions provided by the radar manufacturer for injecting a test signal. During calibration, the
radar should be fully operational, so that all sources of noise are present. Ideally the transmitter
should be turned on during calibration.
Important: Verify with the radar manufacturer that no damage will occur to the signal
generator if the transmitter is running during the calibration.
To perform the calibration, insert signals at steps of 5 or 10 dB over the entire range of the
system. Draw the plot shown in figure 5–10. You can utilize fine resolution steps at the ends of
the scale to observer the details of the roll off. Be sure to raise the antenna up a few degrees to
avoid ground thermal noise. Also tune the frequency of the signal generator using the setup
command “pr”, and displaying the received signal spectrum. Be sure to check the tuning at the
end of the calibration to make sure the signal generator and IFD have not drifted apart.
Each time that a new signal level is injected, the measured power values are obtained by first
invoking the SNOISE command and then reading-back the results using the GPARM command.
The Log of Measured Noise Level (Word 6) from GPARM should be used. This procedure
averages many samples together. For IRIS users, this is all handled by the zauto utility.
Finally turn it all the way down and make one more sample to measure the noise level N. I
is
o
obtained from the intercept of the horizontal line at N and the straight line fit to the linear
portion of the curve. This value must be corrected for losses as discussed in the section below.
5.4.2 Single-Point Direct Method for Calibration of
I
o
This calibration method requires no support software. The approach uses the TTY setups
commands. Again the signal generator output must be calibrated in absolute dBm. Use a power
meter to check the calibration.
5–45

RVP8 User’s Manual
March 2006
Processing Algorithms
S Turn the radiate off and connect the signal generator to the test signal injection point.
S Raise the antenna to at least 20 degrees, and set the azimuth to point away from any
known RF sources including the sun.
S Select the pulse width using the mt command.
S Select the pr command and use the commands to set the following:
Plotting Received Power Spectrum...
Rx:Pri, Zoom:x1–x8, Navg:25, Start:100.01 usec (14.99 km), Span:50 usec
S Set the signal generator to the approximate radar RF frequency with a power level
corresponding to a strong signal (30 dB above the noise), and use a CW signal (not a
pulse). This signal should be visible as a peak in the spectrum display. Adjust the siggen
RF signal frequency so that produces the precise IF frequency (e.g., IF frequency of 30
MHz).
S Turn the signal generator off and record the “Filtered” power level. Note that because of
the large averaging it will require several seconds for the average to stabilize.
S Turn the signal generator on, verify that the peak is still at the IF frequency and adjust
the power level to obtain precisely 3 dB more “Filtered” power than was observed with
the noise only. Again, allow several seconds for the averaging to stabilize after you make
each amplitude adjustment.
This is the value of I
to correct the value of I
, i.e., the test signal signal power equals the noise power. The next step is
o
for losses as discussed in the section below.
o
5.4.3 Treatment of Losses in the Calibration
In the calibration of the dBm level of the test signal, be sure to account for any losses that may
occur between the antenna feed and the injection point, and in the cable and coupler that is used
to connect the signal generator to the injection point. Figure 5–11 illustrates the nomenclature of
the various losses that are involved in the calibration. The relationship between the injected test
signal and the value of the received power relative to the feed is:
dBm
dBm
For example, assume the following:
Loss between the feed and the coupler
Loss caused by the coupler
Loss in the cable from siggen to coupler
Then if the test signal generator output is –50 dBm, the injected power is
Feed
Feed
+ dBm
+ dBm
Injected
Siggen
) dBL
* dBL
Feed:Coupler
Coupler
* dBL
dBL
dBL
dBL
Cable
Feed:Coupler
Coupler
Cable
) dBL
Feed:Coupler
3 dB
30 dB
2 dB
dBm
= –50–[30+2]= –82 dBm.
Injected
5–46

RVP8 User’s Manual
March 2006
The equivalent power at the feed is then 3 dB more than this
Processing Algorithms
dBm
= –82+3 = –79 dBm.
Feed
During the calibration, there are several ways to handle the losses using these equations. Two
examples are:
S Each signal generator value can be corrected for losses so that the calibration plot shows
IFD measured power vs received power at the feed. This is recommended for manual
calibration.
S The signal generator values can be plotted directly and the intercept power I
can be
o
corrected for losses so that it is properly referenced to power at the feed. This is the
approach used by the IRIS zauto utility.
Figure 5–11: Illustration of Losses that Affect LOG Calibration
dBm
Feed
Feed
P
t Feed
Transmit
Path
Coupler Receiver
Receive Path
L
Feed:Coupler
L
t
RVP7
IFD
L
Cable
Sig Gen
dBm
siggen
5.4.4 Determination of
Coupler
dBZ
o
Transmitter
P
t
L
The calibration reflectivity is determined from the radar equation as follows:
2
dBZo+ 10 logƪCr
ƫ
I
o
o
where Io is in mW (corrected for receive losses), the reference range ro is 1 km, and the radar
constant C is:
16l2
L
t
2
C +
2.69 10
PttqfG
5–47

RVP8 User’s Manual
March 2006
where,
l Radar wavelength in cm.
Processing Algorithms
P
t
L
t
Transmitted peak power in kW.
Transmit loss (e.g., 3 dB corresponds to L
+ 2)
t
t Pulse width in microseconds.
q Horizontal half-power full beamwidth.
f Vertical half-power full beamwidth.
G Antenna gain (dimensionless) on beam axis.
The radar constant is determined from the characteristics of your radar (check with the
manufacturer if you are unsure of the values). Note that transmit losses are accounted for in the
radar constant, while receiver loss is usually included in the calculation of I
Finally, if the value of I
I
as follows:
o
dBI
o corrected
Example Calculation of
calculated above was not based on loss-corrected dBm values, correct
o
+ dBIo* dBL
dBZ
:
o
Coupler
* dBL
Cable
) dBL
.
o
Feed:Coupler
This sample calculation is provided so that programmers can check their arithmetic. The radar
parameters:
l Radar wavelength in cm. 5 cm.
P
t
L
t
t Pulse width in microseconds 1 microsecond
q Horizontal half-power beamwidth in degrees 1 degree
f Vertical half-power beamwidth in degrees 1 degree
G Antenna gain (dimensionless) on beam axis 19,953 (43.0 dB)
Transmitted power in kW. 500 kW
Transmit Loss 2 (3 dB)
The radar constant for this example is,
16
C +
2.69 10
16l2
PttqfG
+ 6.76 10
L
t
2
6
ƪ
mm6m*3km*2mW
(2.69 10
+
(500)(1)(1)(19,953)
Assume that Io with loss correction is calculated to be –105 dBm (3.16 10
dBZ
is,
o
2
dBZo+ 10logƪCr
ƫ
I
+ 10logƪ(6.76 106)(1)2(3.16 10
o
o
)(5)
*1
2
(2.0)
2
ƫ
*11
mW), then
*11
ƫ
)
+*36.7dB (mm6m*3)
This value would be down-loaded to the signal processor using the SOPRM command.
5–48

RVP8 User’s Manual
March 2006
Processing Algorithms
5.5 Dual PRT Processing Mode
The RVP8 supports two major modes for Dual PRT processing, i.e., algorithms using triggers
that consist of alternate short and long periods. Most of the Doppler parameters are available in
each of these modes. You may also request time series data in both cases; the samples will be
organized so that the first pulse of a short PRT pair always comes first.
5.5.1 DPRT -1 Mode
The DPRT-1 trigger consists of a very short PRT from which Doppler data are obtained,
followed by a much longer PRT whose purpose is to limit the average duty cycle of the
transmitter. No information is extracted from the long PRT pair, but Dual-PRF techniques can
still be used by varying the short period from ray to ray. The “-1” suffix in the name for this
mode is a reminder that Doppler parameters are computed from the short PRT only. The
DPRT-1 mode is intended for millimeter wavelength radars that must run at a very high effective
PRF (up to 20KHz) to get an acceptable unambiguous velocity, but which also have a much
lower duty cycle constraint on the average number of pulses transmitted each second.
In DPRT-1 mode the requested PRF from the host computer will generally be quite large (up to
20KHz); and the reciprocal of this “effective instantaneous PRF” will determine the trigger’s
short PRT interval. In this way, all subsequent physical calculations will be scaled correctly,
e.g., unambiguous velocity, maximum first trip range, etc., are all supposed to be based on the
short PRT interval. The host computer must therefore be configured so that it can ask for these
very high trigger rates.
The duration of the long PRT interval is not specified directly by the host computer. Rather, the
RVP8’s “Maximum number of Pulses/Second” setup parameter is used to compute how much
delay to insert in order to insure that the transmitter’s duty cycle is not exceeded. This special
treatment applies only in DPRT mode; all other modes that have uniform triggers continue to
interpret the RVP8’s trigger bound as a simple “Maximum PRF”.
Since DPRT-1 mode uses only the short pairs of pulses, it is not possible to run the “R2” moment
estimation algorithms. The RVP8 will return the GPARM “Invalid Processor Configuration” bit
if “R2” is requested in DPRT mode. The error bit will also be returned if the number of pulses
requested (sample size) is not even. All other error conditions are the same as FFT mode.
Warning: Since the RVP8’s “Maximum number of Pulses/Sec” is used to enforce
the duty cycle limit, it is essential that it not be overwritten by the host
computer’s upper PRF limit, which typically will be much higher. To insure
this, you must make sure that the PWINFO command is disabled in the RVP8
“Mc” setup menu. You will have no duty cycle protection if you do not do this.
Note: You may still choose to run Dual-PRF velocity unfolding within the
DPRT-1 mode. What will happen is that the short PRT will vary in the selected
3:2, 4:3, or 5:4 ratio, but the overall duty cycle will remain constant. The
combination of Dual–PRF and DPRT-1 is tremendously effective in extending
the radar’s unambiguous velocity interval.
5–49

RVP8 User’s Manual
March 2006
Processing Algorithms
5.5.2 DPRT -2 Mode
The trigger consists of alternating short and long period pulses, where the ratio of the periods is
determined by the velocity unfolding ratio that has been selected. Doppler data are extracted
from both the short and long pulse pairs (hence the “-2” suffix), and unfolded velocities are
made available on each ray based on the combined PRT data from that ray alone. DPRT-2 mode
is intended for rapidly scanning radars where the ray-to-ray spatial continuity assumptions of the
traditional Dual-PRF algorithms do not apply.
The DPRT-2 velocity unfolding algorithm uses a modified version of the standard Dual-PRF
algorithm. Both start by computing a simple velocity difference as a first approximation of the
unfolded result. The standard algorithm uses that difference to unfold the velocity from the most
recent ray, which yields a lower variance estimate than the difference itself. The DPRT-2
algorithm is similar, except that the folded velocity from both PRTs are unfolded independently
and then averaged together.
In addition to the above, the RVP8 also computes the DC average of the (I,Q) data within each
bin. This is used as a simple estimate of clutter power, so that corrected reflectivities are
available in DPRT-2 mode whenever a non-zero clutter filter is selected. DPRT-1 mode is the
same in this respect. However, the DPRT-2 widths use an improved algorithm based on the two
different PRTs, and which avoids the SNR sensitivity of the DPRT-1 width estimator.
5–50

RVP8 User’s Manual
March 2006
5.6 Dual PRF Velocity Unfolding
Processing Algorithms
For a radar of wavelength l operating at a fixed sampling period t
+ 1ńPRF, the unambiguous
s
velocity and range intervals are given by:
+
l
and R
4t
s
u
+ c
V
u
t
s
2
where “c” is the speed of light. Often these intervals do not fully cover the span of velocity and
range that one would like to measure. The problem is generally worse for short wavelength
radars, since that unambiguous velocity span is directly proportional to
unambiguous range interval is made sufficiently large by increasing
t
l for a given t
, then the resulting
s
. If the
s
velocity span may be unacceptably small.
The RVP8 provides a built-in mechanism for extending the unambiguous velocity span by a
factor of two, three, or four beyond that given above. The technique, called Dual PRF velocity
unfolding, uses two pulse periods rather than one, and relies on the extra information thus
obtained to correct (i.e. unfold) the mean velocity measurement from each individual period.
The Dual PRF trigger pattern consists of alternating (N+k)-pulse intervals where the period in
each interval is either
t
(for the low-PRF) or th (for the high-PRF). Here “N” is the sample
l
size, and “k” represents a delay that permits the clutter filter to equilibrate to the new PRF after
each change. The clutter filter impulse response lengths vary according to which filter is
selected.
t
The two trigger periods
give factors of two, three, and four times velocity expansion over the
and th must be chosen in either a 3:2, 4:3, or 5:4 ratio. These ratios
l
t
period alone. The
h
unfolding algorithm makes use of the following results. Suppose that the radar observes a target
with mean velocity V at each of the two trigger periods. The measured phase angles for the
R
autocorrelations at the two PRFs are:
1
ql+
where angles outside the basic
additions of
measurements, and the
" 2p. These angles correspond to the ordinary single-PRF Doppler velocity
" 2p uncertainties reflects the fact that each measurement is folded
4p V t
[
* p, p
l
and q
l
]
interval are returned to that interval by appropriate
h
+
4p V t
l
h
into its own unambiguous interval:
+
l
and V
4t
l
uh
V
ul
+
4t
l
h
If we define f to be the difference between the two measured phases then:
f + ql* qh+
l
ƪ
tl* t
ƫ
h
4p
which can be interpreted as a phase angle within the unfolded interval:
V
u unfold
+
5–51
4(t
l
l
* t
)
h

RVP8 User’s Manual
March 2006
Now if tl and figureth are in a 3:2 ratio, then:
Processing Algorithms
tl* th+
and thus V
u unfold
+ 3Vul+ 2V
The angle f represents a velocity phase angle in
t
l
3
[
* p, p
t
h
+
2
uh
]
, but with respect to an enlarged
unambiguous interval. Thus, by simply differencing the folded angles from the high and low
PRFs, we obtain an angle that is unfolded to a larger velocity span. Similar reasoning shows that
the 4:3 ratio gives a factor of three improvement over
V
, and 5:4 gives a factor of four.
uh
In practice, the unfolded angle f is not in itself a suitable velocity estimator. The reason is that
the variance of
f is equal to the sum of the variances of each of its components, i.e., twice that
of the individual measurements alone. If the target is at all noisy, then this increase in variance
can be severe. Rather than use
f directly, the RVP8 uses it only as a rough estimate in
determining how to unfold the individual velocity measured from each PRF.
Figure 5–12: Dual PRF Concepts
ql* q
h
ql* q
h
Region I
Result
q
ń3
l
Region III
Region I
Result
q
ń2
h
Region II
Region II
Low PRF Case High PRF Case
This technique is illustrated in Figure 5–12. The figure shows how the low-PRF and high-PRF
angles are unfolded based on the difference angle. The diagrams show phase planes representing
the large unfolded velocity interval, and the locations of various vectors on those planes.
Referring first to the right figure, the difference angle is plotted, and the plane is divided into
two equal size regions, one of which is centered on the difference vector. The high-PRF angle is
then divided by two and plotted. The resultant unfolded velocity angle must either be this vector,
or this vector plus
p . Since adding p places the vector into acceptance Region 1 where it is
5–52

RVP8 User’s Manual
March 2006
Processing Algorithms
nearest the difference angle, we conclude that this is the correct unfolding. Likewise, on the left
diagram we unfold the low-PRF angle by dividing the plane into thirds centered on the
difference angle. The result angle is either
q
l
3
q
2p
,
l
)
3
3
or
q
4p
l
)
3
3
depending on which one falls into the acceptance Region 1. Note that the resultant angle is the
same in each case.
The RVP8 makes efficient use of the incoming data by unfolding velocities from both the low
and the high-PRF data, making use each time of information in the previous ray. When low-PRF
data are taken the derived velocities are unfolded by combining information from the previous
high-PRF interval. Likewise, when high-PRF data are acquired the velocities are unfolded based
on the previous low-PRF interval. Thus, when operating in the Dual PRF mode, the RVP8
outputs one data ray for each (N+k)-pulse interval. However, the velocity data in the Dual PRF
rays are unfolded, so that the [–1,+1] interval now represents either two or three times the prior
velocity range. Put another way, the data are still interpreted as described in the section on mean
V
velocity estimation, except that
is now larger.
u
The width data are also modified somewhat during Dual PRF unfolding. Although valid widths
are obtained independently on all rays, those measured at low-PRF are larger than those at
high-PRF. This is simply because the dimensionless width units are with respect to a larger
velocity interval in the latter case. To compensate for this, low-PRF widths are multiplied by
either 2/3 or 3/4 before being output. This puts them in the same scale as the high-PRF values,
and thus, the widths do not vary on alternate pulses. A useful consequence of this is that width
data can be sent directly to a color display generator without having to plot every other ray in a
different scale.
There are a few words of caution that should be kept in mind when using the RVP8 in the Dual
PRF processing modes. The unfolding algorithms make the assumption that targets are
more-or-less continuous from ray to ray. Otherwise, it would not make sense to use data from a
previous ray to unfold velocities in the current ray. Users must therefore assure that their antenna
scan rate and beamwidth are such that each target is illuminated, at least partially, over each full
2(N+k)-pulse interval. In practice, a certain amount of decorrelation from ray to ray is
acceptable, since the previous rays are used only to decide into which unfolded interval the
current ray should be placed. Small errors in the previous ray data, therefore, cause no error in
the output. However, large previous-ray errors would lead to incorrect unfolding.
A more subtle side effect of Dual PRF processing arises from clutter filtering because clutter
notches now appear at several locations in the unfolded velocity span, rather than just at zero
velocity. These additional rejection points come about because the original velocity intervals are
mapped some integer number of times to create the unfolded interval. Since each original
interval has a clutter notch at DC, it follows that the final expanded velocity interval will have
several such notches. For example, in the 3:2 case, in addition to removing DC the clutter filter
removes velocities at
* 2Vuń3, ) 2Vuń3, and V
.
u
Unfortunately, these clutter filter “images” are a fundamental consequence of the Dual PRF
processing technique and are not easily removed. They can cause trouble not only for the
velocity unfolding itself, but because the computed clutter corrections to be wrong at the image
5–53

RVP8 User’s Manual
March 2006
Processing Algorithms
points. However, there is a useful work-around in the RVP8 to minimize their impact — turning
the clutter filter off at far ranges where little clutter is expected and using a narrow clutter filter
minimizes the effects of the clutter filter on weather targets.
The 4:3 and 5:4 PRF unfolding ratios are more susceptible to unfolding errors in cases where the
spectrum width is large and/or the SNR is low. The user should experiment with these ratios to
determine which provides the best results for their particular application. Although the RVP8
trigger generator can produce any trigger frequency, only the 3:2, 4:3, and 5:4 ratios can be used
with the built-in unfolding algorithms. The RVP8 still permits other PRT ratios to be explored,
but the unfolding technique must then be manually programmed on the user’s host computer.
Oscilloscope observations of Dual PRF triggers can sometimes be confusing. Figure 5–13 shows
seven possible scope traces (and their associated probabilities) for the RVP8 trigger during Dual
PRF operation. The PRF ratio is 4:3, and the sample size is 50 pulses at the high PRF, and 37
pulses at the low PRF. The signal labelled “SCOP E ” is the composite of these traces, and is what
would actually be seen on an oscilloscope. Notice that there are a number of low probability pulses.
The exact details of the sample sizes and the trigger hold off time can make the low probability
pulses appear to come and go randomly. This is normal, and is no cause for alarm.
Figure 5–13: Example of Dual PRF Trigger Waveforms
47.0%
47.3%
1.0%
1.0%
1.0%
1.3%
1.3%
SCOPE
100% 50% 50% 49% 2.3% 48.6% 48% 2.3% 2.3% 94.3% 2.3% 2.3%
5–54

RVP8 User’s Manual
March 2006
Processing Algorithms
5.7 Random Phase 2nd Trip Processing
5.7.1 Overview
Second trip echoes can be a serious problem for applications when the radar is operated at high
PRF (e.g., >500 Hz). Second trip echoes are caused by the range aliasing of targets. They appear
as false echoes on the display, usually elongated in the radial direction. On Klystron systems
they will have valid Doppler velocities. On magnetron systems, the Doppler velocities are not
valid, but the noise from the 2nd trip echoes can obscure valid first trip velocity information.
The RVP8 has optional random phase processing for the filtering and recovery of second trip
echoes. Details of the technique are proprietary to SIGMET, Inc. However, the general principle
is described here, along with a discussion of the various configuration options to optimize the
algorithm performance.
The information that is used to separate the first and second trip echoes is the phase. For a
magnetron radar, the phase of each pulse is different. This means that when 1st. and 2nd trip
echoes are received simultaneously, the phase of the first trip return is different from the phase
of the second trip return. For a magnetron radar, the RVP8 measures the phase of the transmitted
pulse and the phase locking is done digitally as opposed to the traditionally locking COHO. For
a Klystron radar, the phase is controlled by the RVP8 via a digital phase shifter that is precisely
calibrated. Typically the Klystron COHO is phase shifted so that each transmit pulse has a
different phase. The sequencing is controlled by the RVP8.
5.7.2 Algorithm
Figure 5–14 shows a schematic of the data processing for random phase. The figure shows the
Doppler spectra for the 1st. and 2nd trip in the various processing stages. The vertical scale is in
dB and the horizontal scale is velocity. In this example, the second trip echo is shown as being
stronger than the first trip echo (usually the reverse is true).
Ideal 1st and 2nd Trip Echoes
The ideal 1st and 2nd trip echoes represent the echoes as they would appear individually. The
ideal 1st trip echo is the echo that would be measured if there were no 2nd trip echo interference.
The ideal 2nd trip echo represents what would be measured if there were no 1st trip echo
interference. If there is no interference from the other trip, a standard Klystron system can
measure the ideal spectra, but there is no way to know whether the echoes are in the 1st or 2nd
trip.
Raw 1st and 2nd Trip Echoes
This figure shows how the echoes from the first trip and second trip interfere with each other.
For the case of a standard magnetron system, the first trip echo is coherent, while the second trip
echo is incoherent (white noise) since the phase of the second trip echo is random. This is
because the receiver is phase locked only to the first trip.
5–55

RVP8 User’s Manual
March 2006
Processing Algorithms
Another way to implement a magnetron system is to let the COHO free-run (rather than phase
locking to the transmit pulse), measure the phase of each transmit pulse and digitally correcting
for the transmit phase. Using this digital phase locking technique, the RVP8 can phase lock or
“cohere” to either the first or the second trip.
Using this technique alone, it is possible to distinguish between 1st and 2nd trip echoes for the
case when the echoes are not overlapped. In other words, the echoes will appear as the idealized
1st and 2nd trip echoes. This range de-aliasing effectively doubles the range of the radar. The
problem is that when echoes are overlapped, the noise contamination from the stronger echo will
make it impossible to measure the weaker echo. This is illustrated in the figure. Thus if the first
trip echo has a good signal-to-noise ratio of 10 dB, then the 2nd trip echo will have a signal-to
noise-ratio no better than –10 dB. This is the fundamental problem with using phase alone to
separate the 1st and 2nd trip echoes.
Filtered 1st and 2nd Trip Echoes
Since the strong echo generates noise that obscures the weaker echo, the approach used in the
RVP8 is to filter the echo from the other trip — the whitening filter. This is shown in the figure.
The adaptive whitening filter removes both the clutter and the weather. All of the phase
information for the other trip is then contained in the white noise portion of the spectrum. Note
that the phase information under the coherent echo that is removed will be dominated by the
coherent echo, i.e., the other trip phase information will be contaminated. For this reason, the
filtering should effect as small a region of the spectrum as possible.
5.7.3 Tuning for Optimal Performance
The Random Phase algorithms are controlled by the same collection of setup and operational
parameters that apply to all of the other processing modes, e.g., choice of sample size, clutter
filter, angle sync, calibration, etc. However, a few parameters are special to Random Phase
mode, and these are described below.
Secondary SQI Threshold
In standard Doppler processing, an SQI threshold is normally not applied to Reflectivity data
because it would cause those data to be rejected in regions of high spectral width. In Random
Phase mode we need to relax this convention because reflected power can only be assigned to a
particular trip when it is coherent within that trip. Incoherent echoes, regardless of their
strength, can not be placed into either trip.
Thus, an SQI threshold is required to qualify Reflectivity data in Random Phase mode. The
RVP8 defines a secondary SQI threshold SQI
value simply as:
SQI
+ Offset ) (Slope SQI)
2
Where Slope and Offset are the Random Phase SQI threshold parameters defined in the Mf
setup section. The factory default values are (Slope + 0.50) and (Offset +*0.05), i.e., the
secondary threshold is a little less than half of the standard value. The Random Phase
which is computed from the standard threshold
2
5–56

RVP8 User’s Manual
March 2006
Processing Algorithms
algorithms check whether the SQI of each recovered trip is less than the secondary SQI
threshold, and if so, the LOG portion of the data are rejected. This SQI test is necessary for a
clean LOG picture, but we need to use a more permissive (lower) threshold value than would
usually be applied to the Doppler data alone.
The Slope and Offset values should be adjusted so that the density of speckles in Random Phase
LOG data is approximately the same as the density of speckles in FFT velocity data for a given
primary SQI value. You may then adjust the primary SQI threshold to achieve the appropriate
tradeoff of speckles vs. sensitivity for your system in all modes of operation. Even with proper
adjustment, it is normal for Random Phase dBZ and dBT data to show “holes” in regions of
weather that have high turbulence or shear. These dropouts will usually match up with similar
gaps in the velocity and width data, both of which are traditionally thresholded by SQI.
Maximum Power Ratio Between Trips
The adaptive filtering that is performed on the data for each trip greatly extends the visibility of
a weak echo that is overlapped with a much stronger one. In practice, the filtering process is
often able to remove 25-35dB of dominant power in order to reveal a much weaker echo in the
other trip. The performance depends on many factors, primarily the spectral width of the
dominant echo, and the overall stability of the radar system.
The difficulties of removing a dominant “other trip” echo from a weather signal are analogous to
the challenge of removing a dominant clutter target from that same signal. In both cases we are
trying to extract a weak weather signature using a filtering procedure that relies on the spectral
confinement of the stronger signal. The RVP8 already has a parameter that can be adjusted to
control sub-clutter visibility, i.e., the Clutter-to-Signal Ratio (CSR). Just as the CSR applies to
the clutter filters, it can likewise be used to place similar limits on the depth of visibility of the
adaptive filters.
As an example, suppose that the RVP8 is operating in Random Phase mode at a PRF of 1500Hz,
and is observing widespread weather having uniform intensity in both the first 100Km trip and
the second 100Km trip. If the CSR were set too conservatively at only 15dB, then the algorithm
would generally be blind to second-trip weather in the range interval from 100km to 117.8km.
2
The explanation for this can be found in the 1ńr
geometric correction for weather echo
intensity. At ranges less than 17.8km, the first trip weather would generally dominate the second
trip weather by more than 15dB. Thus, the initial 17.8km ring of second trip data would be
rejected by the CSR criteria. However, if the CSR were increased to 30dB, then the size of this
missing ring would be reduced to only 3.2km.
If the CSR is set too low you will notice an abrupt ring of missing data in the beginning of the
second trip. If set too high, there will be speckles and other spurious effects within this same
interval. The optimum setting should strike a balance between these two effects.
R1 vs. R2 Algorithms
The Random Phase algorithms for adaptive filtering and separation of trips relies on having the
best possible information about the weather’s SNR and spectral width. Thus, the “R2” Doppler
algorithms are always used, regardless of the setting of the R1/R2 flag in the user’s operational
parameters.
5–57

RVP8 User’s Manual
March 2006
Processing Algorithms
Random Phase and Dual PRF
The random phase processing works seamlessly with the dual PRF processing to provide
advanced range and velocity ambiguity resolution. Both the first and 2nd trip echoes can be
recovered and displayed to a maximum range of 2X the unambiguous range corresponding to the
high PRF.
For optimum performance, the 2D 3x3 speckle filter should be used to smooth the 2nd trip
seams that occur for each ray. In fact, this smoothing of the 2nd trip seam makes the dual PRF
random phase mode work even better than the single PRF random phase.
5–58

RVP8 User’s Manual
March 2006
Figure 5–14: Random Phase Processing Algorithm
Ideal 1st Trip Ideal 2nd Trip
Processing Algorithms
Raw 1st Trip with Raw 2nd Trip with
2nd Trip Noise Contamination 1st Trip Noise Contamination
Filtered 1st Trip Filtered 2nd Trip
Inverse Transfrom
and ReĆCohere
Recovered 1st Trip Recovered 2nd Trip
5–59

RVP8 User’s Manual
March 2006
Processing Algorithms
5.8 Signal Generator Testing of the Algorithms
This section describes a variety of IF signal generator tests that can be used to verify correctness
of the RVP8 processing algorithms. These tests are routinely performed at SIGMET whenever
new algorithms and/or major modes are added to the processor. We have include a few of the
test descriptions here so that they can be used by customers who need to debug their systems, or
who want to better understand how they work. Additional tests for receiver sensitivity and
dynamic range can be found in Appendix D.
5.8.1 Linear Ramp of Velocity with Range
Suppose that a continuous-wave IF waveform has an instantaneous frequency f(t) in Hertz
(cycles/sec). Consider a range bin located at time t
t
+ 1ńPRF. The phase measured at that bin on the n
s
within that pulse starting from range zero (since the RVP8 is phase locked to range zero):
nt
within a set of pulses that are separated by
bin
th
pulse will be the integral of the frequency
)t
s
bin
nt
ŕ
f(t)dt
s
Fn+
If we assume that the input frequency is a linear Frequency Modulation (FM) at the rate of M
T
cycles/sec/sec on top of a base frequency
F
n)1
(n)1)t
* Fn+
ŕ
(n)1)t
)t
s
bin
(To) Mt)dt *
s
, then:
o
nt
)t
s
bin
ŕ
(To) Mt)dt + ( M ts) t
nt
s
bin
which, remarkably, is independent of both To and n. Thus, a linear FM input signal produces a
fixed (I,Q) phase difference from pulse-to-pulse at any given range. The magnitude of the phase
difference is proportional to the range, and the slope is
(ĂMĂt
Ă) cycles for each second of delay in
s
range. For example, if the test signal generator is sweeping 100KHz every two seconds, then the
velocity observed at a range of 300km at 250Hz PRF will be:
F
n)1
* Fn+
100 KHz
ǒ
2sec
Ǔ ǒ
1
250
sec
We would thus observe a velocity of (0.8 V
(
Ǔ
300 km
) at 300km, where V
u
)
6.6 m sec
ǒ
1 km
Ǔ
+ 0.40 cycles
Ă is the unambiguous
u
Doppler velocity in meters/sec. Note that these phase difference calculations have made no
assumptions about the RVP8 processing mode, and thus are valid in all major modes (PPP, FFT,
DPRT, RPH), as well as in all Dual-PRF unfolding modes.
Interestingly, this simple FM signal generator will also produce valid second trip velocities that
can be seen during Random Phase processing. This follows from the above analysis because
we’ve never assumed that t
was smaller than ts, i.e., it is fine for the range bin to be located
bin
in any higher-order trip.
5–60

RVP8 User’s Manual
March 2006
Processing Algorithms
5.8.2 Verifying PHIDP and KDP
The PHIDP and KDP processing algorithms can be tested using CW signal sources at IF. In the
alternating-transmitter single-receiver case, a single FM signal generator is modulated with an
RVP8 polarization select line so that slightly different frequencies are generated for the H and V
pulses. A maximum FM depth of several kilohertz is all that is required. In the dual-receiver
case, two (unmodulated) signal generators are used for each of the H and V intermediate
frequencies, and one or the other is detuned slightly from its correct center frequency. In either
case the frequency difference that produces a KDP value of 1.0 degree/km will be:
(1.0
degree
km
) (
1
360
cycles
degree
) ( 299792
km
second
) + 833
cycles
second
5.8.3 VerifyingRHOH, RHOV, and RHOHV
These three terms measure the normalized cross-channel covariance in a polarization radar.
They all are computed in essentially the same way having the form:
n
n
s
RHOAB +
t s
Ǹ
t s
Where the s
n
A
and s
n
are complex (I,Q) vectors from two receiver channels A and B, and “<>”
B
denotes expected value. This suggests that some form of amplitude modulation (AM) of the
input signal might be helpful.
Suppose that the
n
s
A
and s
n
samples are coming from two signal generators installed on a
B
dual-receiver system, and that only the B-Channel is AM modulated so that:
n
| s
| + {SA, SA, SA,SA, SaAAA } ,|s
A
Then the above estimator reduces to:
1
(
) SAS
Ǹ
2
1
2
S
(
2
A
RHOAB +
*u
A
B
2
A
B
) S
2
ut s
n
| + {SB,0,SB,0,SBAAA }
B
u
B
++0.707
2
B
A simple way to create these data is to set the A-Channel siggen for 95% AM depth, and use a
sinusoidal modulation source of, perhaps, 400Hz. The reason for not choosing 100% depth is
that we would loose the Burst phase reference when the amplitude became smallest. The 26dB
reduction in
S
is a close enough approximation to zero in the above formula.
B
If we now observe the two receive channels with the RVP8 at a PRF of 800Hz, we will see the
various RHOAB terms varying with range; reaching a high value of 1.00, and a low value of
0.707. The plots will be nearly stationary on the ascope screen because the PRF is almost
precisely twice the modulation rate (though they are free-running relative to each other).
Adjusting the amplitude of either signal generator will not affect the ò terms, but it will have an
interesting effect on SQI. If (T,Z,V,W) are being computed from both channels combined, then
the SQI is:
2
S
SQI +
2
S
A
5–61
) (
A
1
2
) S
2
B

RVP8 User’s Manual
March 2006
Processing Algorithms
If we solve this equation for SQI=0.5 we find that the individual SA terms must have twice the
power of the individual
S
terms. This can be checked by adjusting either signal generator until
B
the minimum plotted SQI is 0.5, and then verifying that the average H and V powers are
identical; or, equivalently, that ZDR, LDRH and LDRV are zero.
The linear FM ramp described in Section 5.8.1 can also be used as a test of RHOAB in a
dual-receiver system. With one siggen modulated and the other fixed, one receive channel will
appear to be rotating relative to the other. If the FM modulation is such that 1/N of a full
revolution occurs per pulse at a given range, then if the sample size is N pulses we will observe
RHOAB + 0 at that range. In fact, the plot of RHOAB will show a characteristic sin(x)ńx behavior
as a function of range.
5–62
 Loading...
Loading...