ANALOG DEVICES AN-922 Service Manual

AN-922

APPLICATION NOTE

One Technology Way • P. O . Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel : [phone] • Fax: [phone] • www.analog.com

Digital Pulse-Shaping Filter Basics

by Ken Gentile

INTRODUCTION

Data transmission systems that must operate in a bandwidth­limited environment must contend with the fact that constraining
the bandwidth of the transmitted signal necessarily increases
the likelihood of a decoding error at the receiver. Bandwidth
limited systems often employ pulse-shaping techniques that
allow for bandwidth containment while minimizing the
likelihood of errors at the receiver.

Before digital filters were available, pulse shaping was accom­plished with analog filters. Unfortunately, the response of an
analog filter is affected by variations in component values due
to specified tolerance ranges, temperature, and aging. The
response of a digital filter, by contrast, is solely dependent on
the filter coefficients, which are invariant to both temperature
and aging. Therefore, digital pulse-shaping filters have become
an integral part of many digital data transmission systems. This
application note describes the fundamentals of pulse shaping
and the tradeoffs associated with the design of digital pulse­shaping filters.

THE RECTANGULAR PULSE

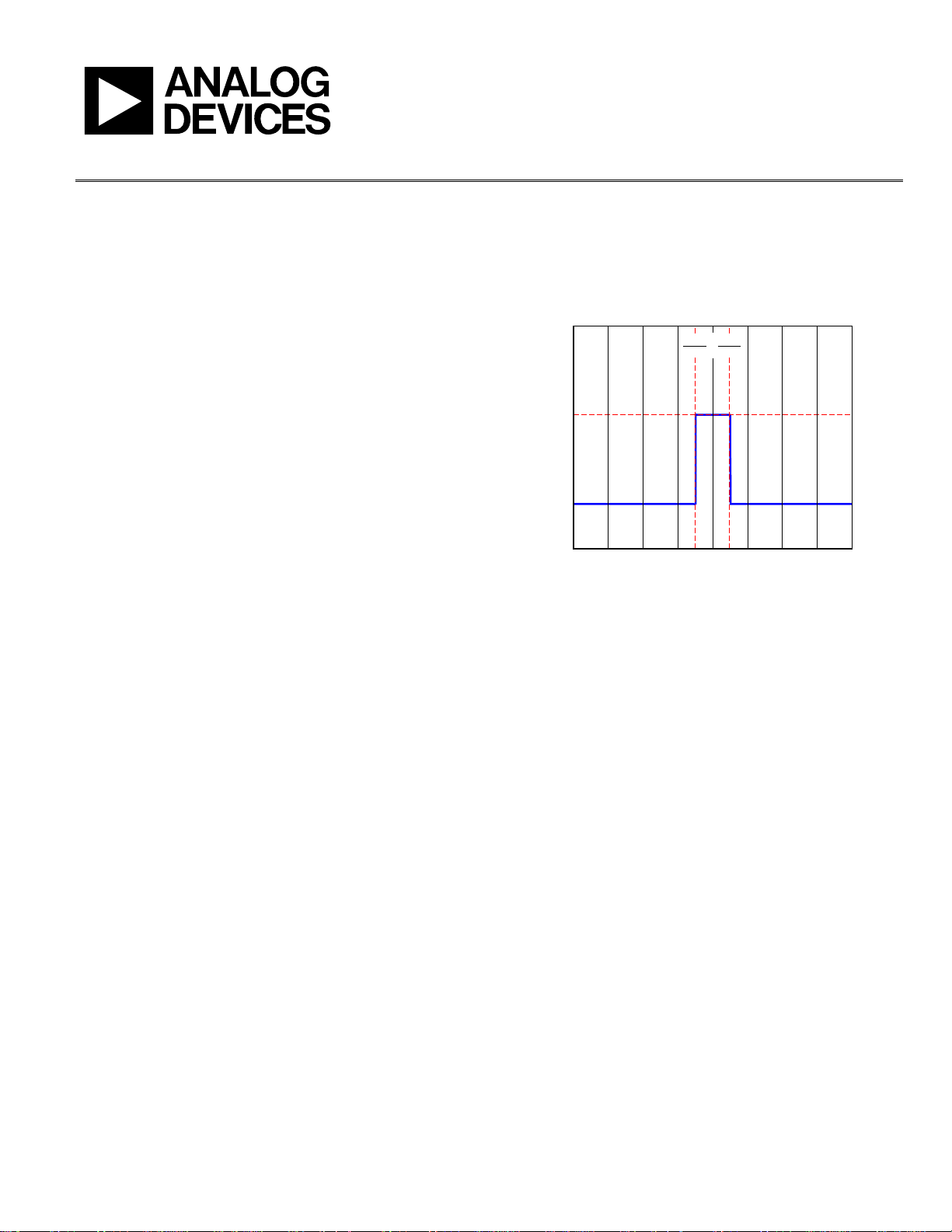
The most basic information unit in a digital transmission
scheme is a rectangular pulse. It has a defined amplitude,
A, and defined duration, T. Such a pulse is shown in
where A = 1, T = T

, with the pulse centered about the time

o

origin at t = 0. Typically, a sequence of such pulses (each
delayed by T seconds relative to the previous one) constitutes
the transmission of information. The information, in this
case, is encoded in the amplitude of the pulse. The simplest
case is when a binary 0 is encoded as the absence of a pulse
(A = 0) and a binary 1 is encoded as the presence of a pulse
(A = constant). Since each pulse spans the period T, the maxi­mum pulse rate is 1/T pulses per second, which leads to a data
transmission rate of 1/T

bits per second.

In more sophisticated data transmission schemes, the pulse
amplitude can take on both positive and negative values with
multiple discrete amplitudes used to encode more than one bit
into the pulse. For example, four levels can be used to encode
two bits in which each level is uniquely associated with one of
the four possible bit patterns. In some cases, multiple pulses are
transmitted simultaneously, which allows even more bits to be
encoded (see the Multibit Symbol Encoding section).

Figure 1,

2

1

AMPLITUDE

0

–4–3–2–101234

RECTANGULAR PULSE (TIME DO MAIN)

–T

T

O

O

2

2

TIME (IN UNITS OF TO)

Figure 1. A Single Rectangular Pulse (T = T

, A = 1)

O

A

06897-001

In sophisticated transmission systems, multiple amplitudes
and/or multiple simultaneous pulses transmit a single unit of
data. As such, each single unit of data can represent more than
one bit. The group of bits that a single unit of data represents is
referred to as a symbol. The trivial case, of course, is the single
bipolar pulse of

Figure 1 where each unit of data is a single bit

(symbol and bit are synonymous in this case).

The pulses used to transmit symbols occupy a fixed time inter­val, T (as in

Figure 1). Thus, the pulse rate is 1/T pulses per
second, which leads to a symbol rate of 1/T symbols per second.
The unit, symbols per second, is often referred to as baud. The
data transmission rate in bits per second is the baud rate
multiplied by the number of bits represented by each symbol.
For example, if a symbol represents four bits, then the bit rate is
four times the symbol rate. This means that a lower transmission
rate can be used to transmit symbols as opposed to directly
transmitting bits, which is the primary reason that the more
sophisticated data transmission systems encode groups of bits
into symbols. The remainder of this application note focuses on
a single bipolar pulse for transmitting one bit at a time. That is, a
logical 1 is represented by the presence of a pulse of unit
amplitude and a logical 0 by the absence of a pulse (that is, zero
amplitude). The concepts discussed in this application note,
however, extend directly to the more sophisticated encoding
schemes.

Rev. 0 | Page 1 of 12

AN-922

TABLE OF CONTENTS

Introduction ...................................................................................... 1

The Rectangular Pulse ..................................................................... 1

Spectrum of a Rectangular Pulse.................................................... 3

The Raised Cosine Filter.................................................................. 3

Pulse Shaping .................................................................................... 4

Digital Pulse-Shaping Filters........................................................... 5

Group 1 Plots: Error at the Edge of the Pass Band........................7

Group 2 Plots: Error at the Nyquist Frequency.............................8

Group 3 Plots: Minimum Stop Band Attenuation ........................9

Multibit Symbol Encoding ............................................................ 10

References........................................................................................ 11

Rev. 0 | Page 2 of 12

AN-922

τ

SPECTRUM OF A RECTANGULAR PULSE

The frequency content (or spectrum) associated with the pulse

Figure 1 is shown in Figure 2. The spectrum of the pulse is

of
obtained by applying the Fourier transform to the time domain
waveform of

Figure 1. The shape of the spectrum is the well­known sin(x)/x response, which is often referred to as the sinc
response. The null points (where the spectral magnitude is
zero) always occur at integer multiples of f

, which is the pulse

O

(or symbol) rate. Therefore, the null points are solely determined
by the pulse period, T. In theory, the nulls and peaks extend in
frequency out to ±∞ with the peaks approaching zero magnitude.
However, because the frequency span of

Figure 2 is only ±4 fO,

only four null points are evident on each side of the f = 0 line.

RECTANGULAR PULSE SPECTRUM

–

f

O

1

PULSE SPECTRUM

MAGNITUDE

0

–4–3–2–101234

FREQUENCY (I N UNITS OF

Figure 2. Spectrum of a Single Rectangular Pulse of Duration T

f

O

T

O

f

)

O

06897-002

o

The general shape of the spectrum that appears in Figure 2 is
the same regardless of the amplitude of the rectangular pulse.
Although the amplitude of the rectangular pulse proportionally
affects the magnitude of the peaks, it has no effect on the
frequency location of the null points. Therefore, encoding
schemes that rely on pulse amplitude variations still produce
a spectrum similar to that of

Figure 2 even though the pulse

amplitude may vary from pulse to pulse.

THE RAISED COSINE FILTER

As shown in Figure 2, the spectrum of a rectangular pulse spans
infinite frequency. In many data transmission applications, the
transmitted signal must be restricted to a certain bandwidth.
This can be due to either system design constraints or govern­ment regulation. In such instances, the infinite bandwidth
associated with a rectangular pulse is not acceptable. The
bandwidth of the rectangular pulse can be limited, however, by
forcing it to pass through a low-pass filter. The act of filtering
the pulse causes its shape to change from purely rectangular to a
smooth contour without sharp edges. Therefore, the act of
filtering rectangular data pulses is often referred to as pulse
shaping.

Unfortunately, limiting the bandwidth of the rectangular pulse
necessarily introduces a damped oscillation. That is, the
rectangular pulse exhibits nonzero amplitude only during the

Rev. 0 | Page 3 of 12

pulse interval, whereas the smoothed (or filtered) pulse exhibits
ripples both before and after the pulse interval. At the receiver,
the ripples can lead to incorrect decoding of the data, because
the ripples associated with one pulse interfere with the pulses
before and after it. However, the choice of a proper filter can
yield the desired bandwidth reduction while maintaining a time
domain shape that does not interfere with the decoding process
of the receiver.

This filter is the well-known raised cosine filter and its
frequency response is given by

H

()

,

()

−ωτ

c

⎡

2

{

τ

=ω

cos

⎢
⎣

⎤

}

,

⎥

α

4

⎦

,0

c

≤ω≤

0

dc

≤ω≤

d

>ω

where:
ω is radian frequency (2πf).
τ is the pulse period (equivalent to T

in Figure 1).

O

α is the roll off factor.

c is equal to π
d is equal to π

(1 − α)/τ.

(1 + α)/τ.

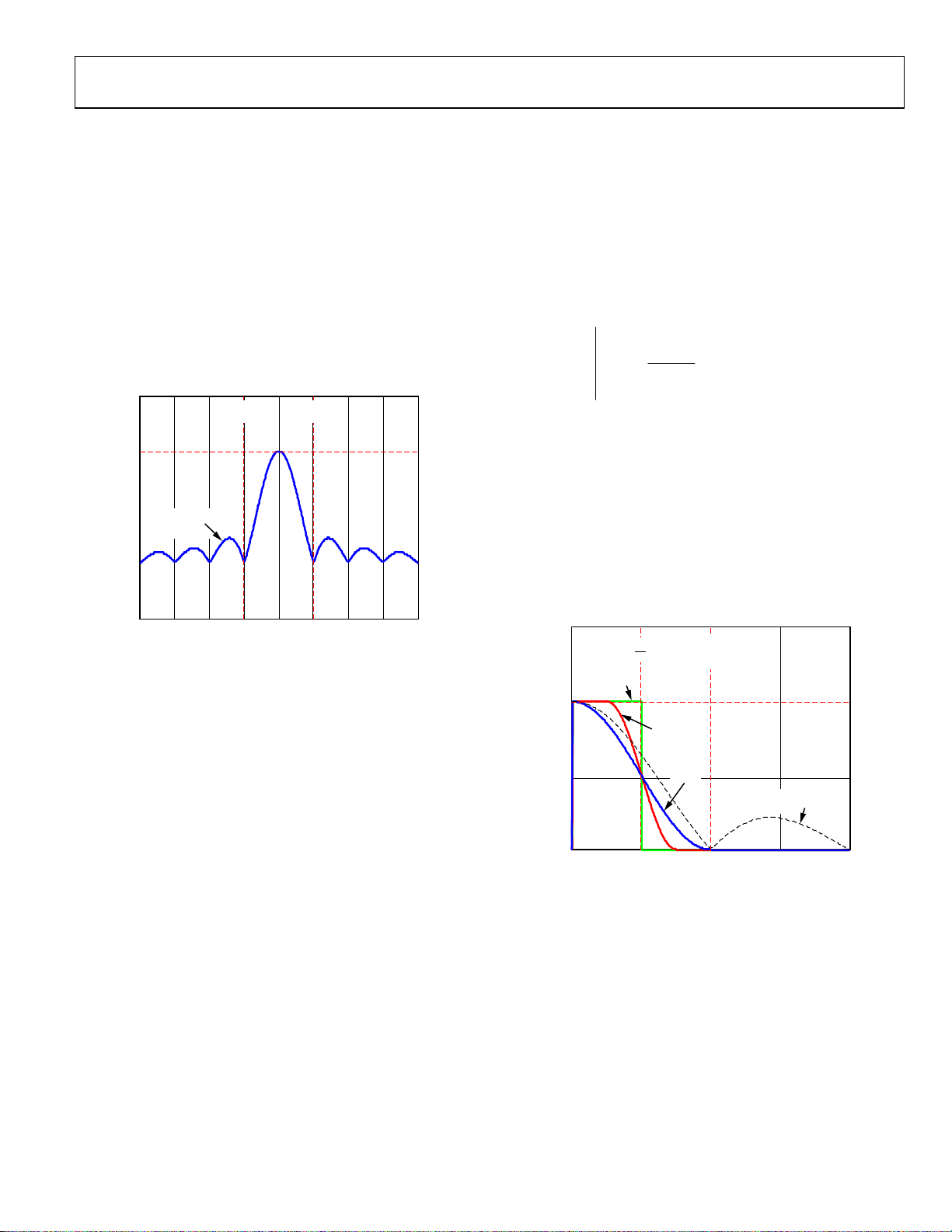
A plot of the raised cosine frequency response is shown in
Figure 3 (normalized to τ = 1). The raised cosine filter gets its
name from the shape of its frequency response, rather than its
impulse (or time domain) response.

1.5

1.0

MAGNITUDE

0.5

0

00.5 1.51.0 2.0

Figure 3. The Raised Cosine Frequency Response

RAISED COSINE SPECTRUM

f

O

2

α

= 0

α

FREQUENCY (NORMALIZED TO SYMBOL RAT E)

= 1/2

f

O

α

= 1

PULSE SPECTRUM

T

O

06897-003

The response characteristic of the raised cosine filter is
adjustable via a parameter known as the roll off factor
represented by the symbol α, where 0 ≤ α ≤ 1.

In the case of α = 0, the frequency response is confined to

(the green trace).

½ f

O

For α = 1, the frequency response is confined to f

(the

O

blue trace).

For values of α between 0 and 1, the frequency response is
restricted to an intermediate range between ½ f

and fO (the

O

red trace shows the response for α = ½).

AN-922

The dashed black trace is the spectrum of a rectangular pulse
and is included for the sake of comparison.

There are three significant frequency points associated with the
raised cosine response. The first is known as the Nyquist frequency,
which occurs at ½ f
communication theory, this is the minimum possible bandwidth
that can be used to transmit data without loss of information.
Note that the raised cosine response crosses through the ½
amplitude point at ½ f
significant frequency point is the stop band frequency (f
defined as the frequency at which the response first reaches
zero magnitude. It is related to α by:

f α+=

STOP

The third, and final, significant frequency point is the pass band
frequency (f

PAS S

first begins to depart from its peak magnitude. The raised
cosine response is perfectly flat from f = 0 (DC) to f

f α−=

PASS

Sometimes it is desirable to implement the raised cosine
response as the product of two identical responses, one at the
transmitter and the other at the receiver. In such cases, the
response becomes a square-root raised cosine response since
the product of the two responses yields the desired raised cosine
response. The square-root raised cosine response is given below.
Note that the variable definitions are the same as for the raised
cosine response.

()

H

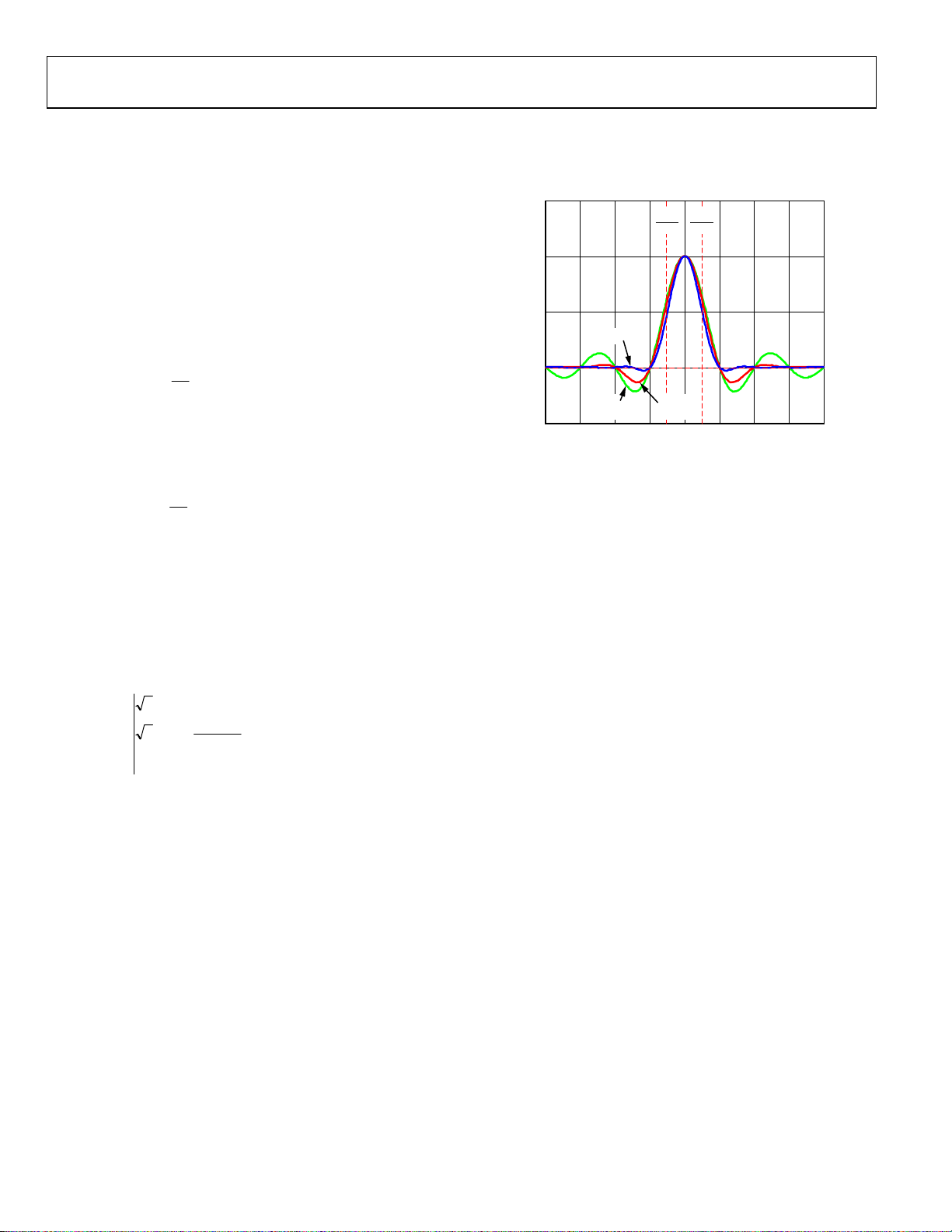
PULSE SHAPING

The consequence of pulse shaping is that it distorts the shape of
the original time domain rectangular pulse into a smoothly
rounded pulse with damped oscillations (ripples) before and
after the ±½ T
of the rectangular pulse with the raised cosine impulse response
(convolution is the process of filtering in the time domain). The
impulse response (time domain) of the raised cosine filter is
shown in
used in
impulse response for α = 0, the red trace for α = ½, and the blue
trace for
is the unavoidable consequence of limiting the bandwidth of the
filter to something less than infinity. However, the beauty of the
raised cosine filter is that the zero crossings of the impulse
response coincide with the midpoint of adjacent pulses. As long
as the receiver makes its decision at the middle of each pulse

Figure 4 where the color scheme is the same as that

Figure 3. That is, the green trace corresponds to the

α = 1. The oscillation observed in the impulse response

(that is, ½ the pulse rate). According to

O

regardless of the value of α. The second

o

)

STOP

f

O

)1(

2

) defined as the frequency at which the response

, where:

PAS S

f

O

)1(

2

,

()

−ωτ

c

⎡

{

ττ=ω

cos

⎢

α

4

⎣

,0

points. The ripples result from the convolution

o

0

c

⎤

}

,

⎥
⎦

≤ω≤

dc

≤ω≤

d

>ω

interval, then the ripples from adjacent pulses are crossing
through zero. Therefore, they do not interfere with the decision
making process.

1.5

1.0

0.5

AMPLITUDE

0

–0.5

–4–3–2–101234

RAISED COSINE TIME DOMAI N RESPONSE

–T

T

O

O

2

2

α

= 1

α

α

= 0

FREQUENCY (NO RMALIZED T O SYMBOL PERIOD)

Figure 4. The Raised Cosine Time Domain Response

= 1/2

06897-004

Note that as α is increased from 0 to 1 the pass band of the filter
is increased (see
domain ripples is decreased (see

Figure 3) while the amplitude of the time

Figure 4). Thus, α = 0 offers
the most efficient use of bandwidth, but this comes at the cost
of more pronounced ripples in the time domain response
(relative to α > 0). Choosing α > 0 causes an increase in the
bandwidth of the transmitted spectrum, but this negative effect
is offset by a reduction of the ripple amplitude in the time
domain response.

The raised cosine response is beneficial because it produces
time domain ripples that cross through zero at the middle of
adjacent pulse intervals. If the raised cosine pulse exhibits zero
crossings at the midpoint of adjacent pulse intervals regardless
of the choice of α, then why be concerned about the ripple
amplitude? Why not just choose α = 0 to get the minimum
bandwidth and accept the maximum ripple amplitude? The
reason is that the receiver is usually not capable of sampling at
exactly the midpoint of each pulse. Since the ripples only
exhibit zero amplitude at the middle of adjacent pulse intervals,
then a receiver sample that is not coincident with the midpoint
of a pulse interval necessarily samples some ripple from
adjacent pulses.

This is a source of decision-making error at the receiver known
as intersymbol interference (ISI). Reduced bandwidth means
larger ripple, which exacerbates ISI and increases the likelihood
of an incorrect decision (that is, error) at the receiver. Obviously,
a trade off exists between bandwidth containment in the fre­quency domain and ripple attenuation in the time domain. It is
this trade off of bandwidth containment vs. ripple amplitude
that must be considered by design engineers when developing a
data transmission system that employs pulse shaping.

Rev. 0 | Page 4 of 12