Page 1
AN-732
V
OUT
R7
R2
R4
R6
VIN1
V
IN
2
APPLICATION NOTE
One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • Tel: 781/329-4700 • Fax: 781/326-8703 • www.analog.com
Universal Precision Op Amp Evaluation Board in SOIC Package
by Giampaolo Marino, Soufi ane Bendaoud, and Steve Ranta
INTRODUCTION
The EVAL-PRAOPAMP-1R is an evaluation board which
accommodates single op amps in SOIC packages. It is
meant to provide the user with multiple choices and
extensive fl exibility for different applications circuits
and confi gurations. This board is not intended to be
used with high frequency components or high speed
amplifi ers. However, it provides the user with many
combinations for various circuit types including active
fi lters, differential amplifi ers, and external frequency
compensation circuits. A few examples of application
circuits are given in this application note.
C7
R7
R2
V
GAIN (dB)
60
40
20
0
–20
IN
R7/R2 = 100
f
R6
f
C
10f 100f 1000f 10000f
RELATIVE FREQUENCY
V
OUT
f
L
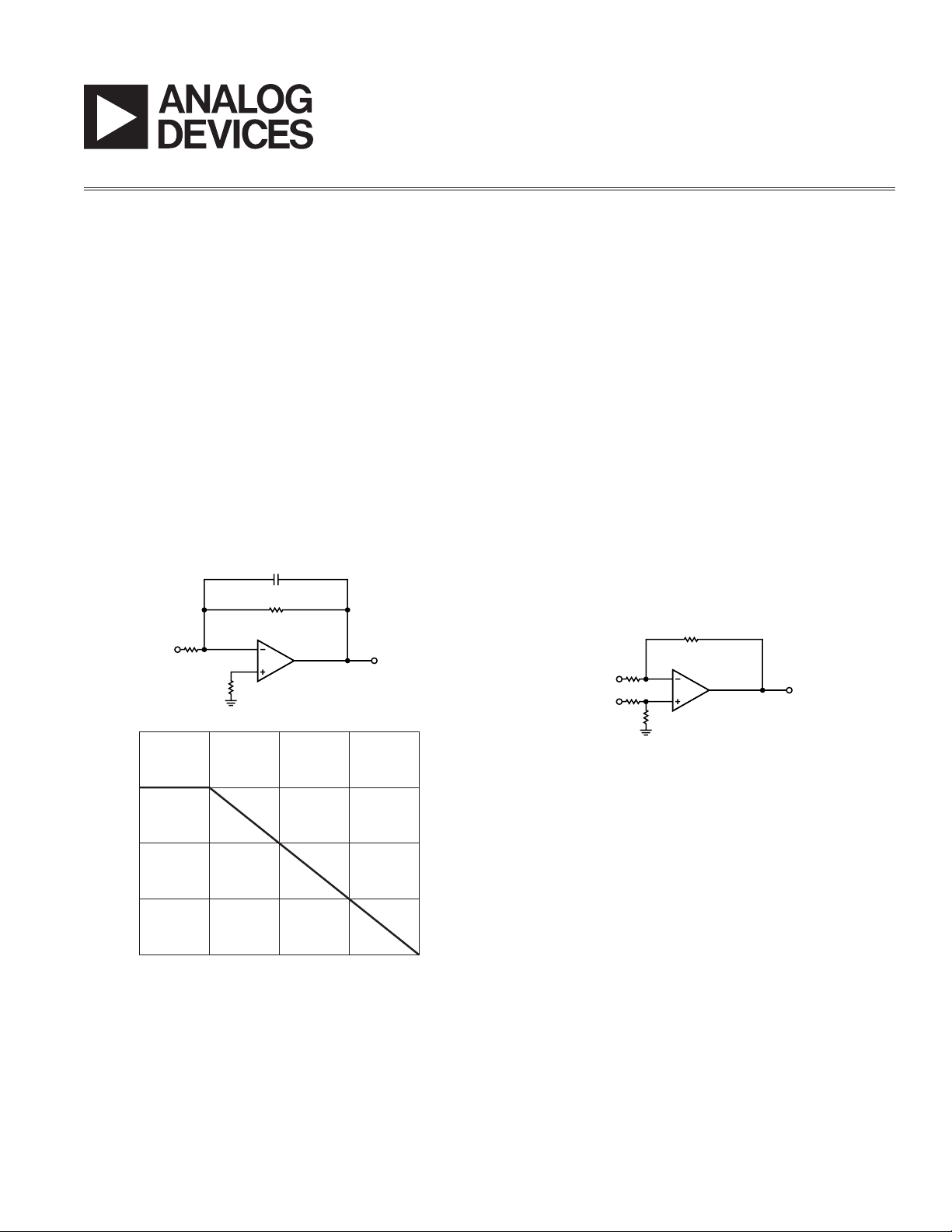
Figure 1. Simple Low-Pass Filter
LOW-PASS FILTER
Figure 1 is a typical representation of a fi rst-order lowpass fi lter. This circuit has a 6 dB per octave roll-off
after a close - loop –3 dB point defi ned by f
. Gain below
C
this frequency is defi ned as the magnitude of R7 to R2.
The circuit might be considered as an ac integrator for
frequencies well above fC; however, the time domain
re
sponse is that of a single RC, rather than an integral.
= 1/(2 R7 C7); –3 dB frequency
f
C
= 1/(2 R2 C7); unity gain frequency
f
L
Acl = –(R7/R2); close loop gain
R6 should be chosen equal to the parallel combination
between R7 and R2 in order to minimize errors due to
bias currents.
Figure 2. Difference Amplifi er
DIFFERENCE AMPLIFIER AND PERFORMANCE OPTIMIZATION
Figure 2 shows an op amp confi gured as a difference
amplifi er. The difference amplifi er is the complement
of the summing amplifi er, and allows the subtraction
of two voltages or the cancellation of a signal common
to both inputs. The circuit shown in Figure 2 is useful
as a computational amplifi er in making a differential
to single-ended conversion or in rejecting a commonmode signal. The output voltage V
is comprised of
OUT
two separate components:
1. A component V
1 due to VIN1 acting alone (VIN2
OUT
short- circuited to ground.)
2. A component V
2 due to VIN2 acting alone (VIN1
OUT
short- circuited to ground.)
REV. A
Page 2
AN-732
V
OUT
R7
R6
IIN1
V
OUT=IIN
1 ⴛ R7
The algebraic sum of these t wo components should be
equal to V
the output voltage V
. By applying the principles expressed in
OUT
components, and by letting R4
OUT
= R2 and R7 = R6, then:
V
1 = VIN1 R7/R2
OUT
2 = –VIN2 R7/R2
V
OUT
V
= V
OUT
OUT
1 + V
2 = ( VIN1 – VIN2) R7/R1
OUT
Difference amplifiers are commonly used in high
accuracy circuits to improve the common-mode rejec tion ratio, typically known as CMRR.
For this type of application, CMRR depends upon how
tightly matched resistors are used; poorly matched resistors result in a low value of CMRR.
To s e e h ow this works, consider a hypothetical source
of error for resistor R7 (1 – error). Using the superposition principle and letting R4 = R2 and R7 = R6, the output
voltage would be as follows:
7
R
2
R
V
OUT
=
VD
VV V
227
RR
1
−
RR
+
27
RR
=−21
DD IN IN
+
27 2
R
+
×
+
7
×
error
error
CURRENT-TO-VOLTAGE CONVERTER
Current may be measured in two ways with an operational amplifi er. Current can be converted to a voltage
with a resistor and then amplifi ed or injected directly
into a summing node.
Figure 3. Current-to-Voltage Converter
Figure 3 is a typical representation of a current-to-voltage
transducer. The input current is fed directly into the sum ming node and the amplifi er output voltage changes to
exactly the same current from the summing node through
R7. The scale factor of this circuit is R7 volts per amps.
The only conversion error in this circuit is I
summed algebraically with I
C9
V–
R4
V+
1.
IN
R7
V
OUT
, which is
BIAS
From this equation, ACM and ADM can be defi ned as
follows:
A
= R7/(R7 – R2) error
CM
= R7/R2 {1 – [(R2+2R7/R2+R7) error/2]}
A
DM
These equations demonstrate that when there is not an
error in the resistor values, the A
= 0 and the amplifi er
CM
responds only to the differential voltage being applied to
its inputs; under these conditions, the CMRR of the circuit
becomes highly dependent on the CMRR of the amplifi er
selected for this job.
As mentioned above, errors introduced by resistor
mismatch can be a big drawback of discrete differential
amplifi ers, but there are different ways to optimize this
circuit confi guration:
1. The dif ferential gain is directly related to the ratio R7/
R2; therefore, one way to optimize the performance
of this circuit is to place the amplifi er in a high gain
confi guration. When larger values for resistors R7 and
R6 and smaller values for resistors R2 and R4 are se lected, the higher the gain, the higher the CMRR. For
example, when R7 = R6 = 10 k, and R2 = R4 = 1 k, and
error = 0.1%, CMRR improves to better than 80 dB. For
high gain confi guration, select amplifi ers with very
low I
and very high gain (such as the AD8551,
BIAS
AD8571, AD8603, and AD8605) to reduce errors.
2. Select resistors that have much tighter tolerance and
accuracy. The more closely they are matched, the better
the CMRR. For example, if a CMRR of 90 dB is needed,
then match resistors to approximately 0.02%.
R9
Figure 4. Bistable Multivibrator
L+
BL+=V
TH
BL–=V
L–
TL
Figure 5. Output Response
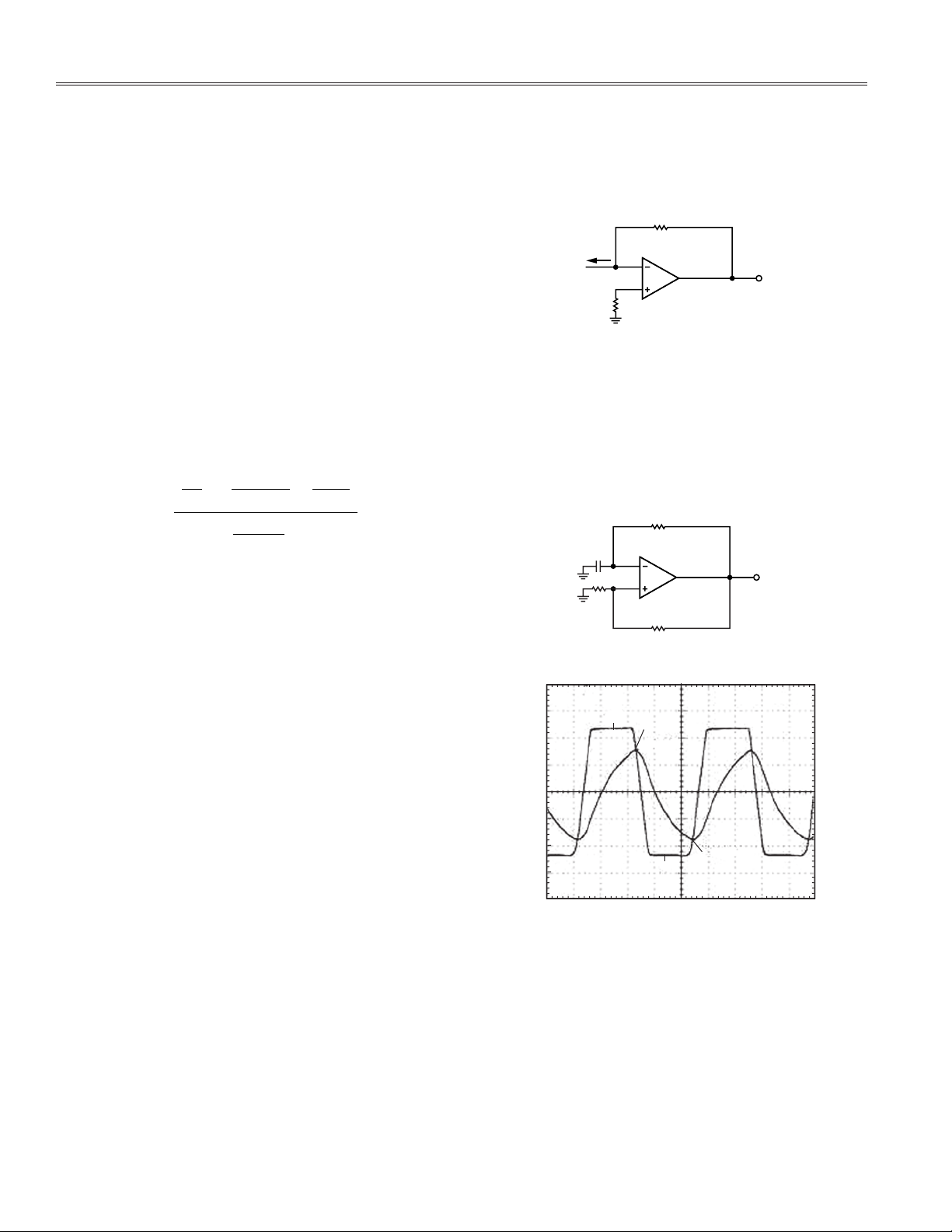
GENERATION OF SQUARE WAVEFORMS USING A BISTABLE MULTIVIBRATOR
A square waveform can be simply generated by arranging the amplifi er for a bistable multivibrator to switch
states periodically as Figure 5 shows.
Once the output of the amplifi er reaches one of two possible levels, such as L+, capacitor C9 charges toward this
level through resistor R7. The voltage across C9, which
is applied to the negative input terminal of the amplifi er denoted as V–, then rises exponentially toward L+
with a time constant = C9R7. Meanwhile, the voltage
–2–
REV. A
Page 3

AN-732
at the positive input terminal of the amplifi er, denoted as
V+ = BL+. This continues until the capacitor voltage
reaches the positive threshold VTH, at which point
the bi
stable multivibrator switches to the other stable
state in which V
= L– and V+ = BL–. This is shown in
O
Figure 5.
The capacitor then begins to discharge, and its voltage,
V–, decreases exponentially toward L–. This continues
until V– reaches the negative threshold V
, at which time
TL
the bistable multivibrator switches to the positive output
state, and the cycle repeats itself.
It is important to note that the frequency of the square
wave being generated, f
, depends only on the external
O
components being used. Any variation in L+ will cause
V+ to vary in proportion, ensuring the same transition
time and the same oscillation frequency. The maximum
operating frequency is determined by the amplifier
speed, which can be increased signifi cantly by using
faster devices.
The lowest operating frequency depends on the practical
upper limits set by R7 and C9.
Using the name convention outlined on the PRA OPAMP
evaluation board, the circuit should be connected as
fol
lows:
B = R4/(R4 + R9); feedback factor (noninverting input)
T = 2R7 C9 ln((1 + B)/(1 – B)); period of oscillation
= 1/T; oscillation frequency
f
O
RL= 10k⍀
CL= 2nF
GND
VOLTAGE (200mV/DIV)
TIME (10s/DIV)
Figure 8. Capacitive Load Drive with Resistor
EXTERNAL COMPENSATION TECHNIQUES
Series Resistor Compensation
The use of external compensation networks may be
required to optimize certain applications. Figure 6 is a
typical representation of a series resistor compensation
for stabilizing an op amp driving capacitive load. The
stabilizing effect of the series resistor isolates the op amp
output and the feedback network from the capacitive
load. The required amount of series re sistance depends
on the part used, but values of 5 to 50 are usually
suffi cient to prevent local resonance. The disadvantages
of this technique are a reduction in gain accuracy and
extra distortion when driving nonlinear loads.
R02
C
V
IN
LRL
V
OUT
Figure 6. Series Resistor Compensation
RL= 10k⍀
CL= 2nF
GND
VOLTAGE (200mV/DIV)
TIME (10s/DIV)
Figure 7. Capacitive Load Drive Without Resistor
V
R
CLR
V
IN
S
C
S
L
OUT
Figure 9. Snubber Network
GND
VOLTAGE (200mV/DIV)
TIME (10s/DIV)
Figure 10. Capacitive Load Drive Without Snubber
REV. A
–3–
Page 4

AN-732
RL= 10k⍀
CL= 500pF
RS= 100⍀
CS= 1nF
VOLTAGE (200mV/DIV)
TIME (10s/DIV)
Figure 11. Capacitive Load Drive with the Snubber
*THESE COMPONENTS ARE BY DEFAULT
SHORTED WITH A SMALL COPPER
STRAP BETWEEN THE MOUNTING PADS.
TO USE THE COMPONENT MOUNTING
LOCATION, SIMPLY REMOVE THE STRAP
WITH A CUTTING UTENSIL (DREMEL
CUTTING TIP, EXACTO BLADE, ETC.)
G1
G2
C2
*R1
V1
R
0
V2
RT2
0
*R2
1
T
R3
*R4
C9
R10
R5
C5
R6 C6
C1
2
3
*R11
C7
R7
VCC
V+
V–
7
4
*R12
DUT
R9
Snubber Network
Another way to stabilize an op amp driving a capacitive
load is with the use of a snubber, as shown in Figure 9.
This method presents the signifi cant advantage of not
reducing the output swing because there is not any
isolation resistor in the signal path. Also, the use of
the snubber does not degrade the gain accuracy or
cause extra distortion when driving a nonlinear load.
The exact R
and CS combinations can be determined
S
experimentally.
ALL PASSIVE COMPONENT MOUNTING
LOCATIONS CAN ACCOMMODATE 0805 TO 2512
SIZED SURFACE MOUNT PACKAGES, 1/2" SPACED
LEADED RESISTORS AND 0.3" SPACED
*C8
LEADED CAPACITORS
R8
C10
6
C11
G3
*R
O
G4
*RO1 *RO2
R
S
C
S
VO
R
C
L
L
G5
AN04894–0–8/04(A)
VEE
Figure 12. EVAL-PRAOPAMP-1R Electrical Schematic
Figure 13. EVAL-PRAOPAMP-1R Board Layout Patterns
© 2004 Analog Devices, Inc. All rights reserved. Trademarks and registered trademarks are the property of their respective owners.
–4–
REV. A
 Loading...
Loading...