Analog Devices AN-279 Application Notes

AN-279

a

APPLICATION NOTE

One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • 781/329-4700 • World Wide Web Site: http://www.analog.com

Using the AD650 Voltage-to-Frequency Converter As a

Frequency-to-Voltage Converter

By Steve Martin

The AD650 is a versatile monolithic voltage-to­frequency converter (VFC) that utilizes a charge­balanced architecture to obtain high performance in
many applications. Like other charge-balanced VFCs,
the AD650 can be used in a reverse mode as a
frequency-to-voltage (F/V) converter. This application
note discusses the F/V architecture and operation,
component selection, a design example, and the
fundamental trade-off between output ripple and circuit
response time.

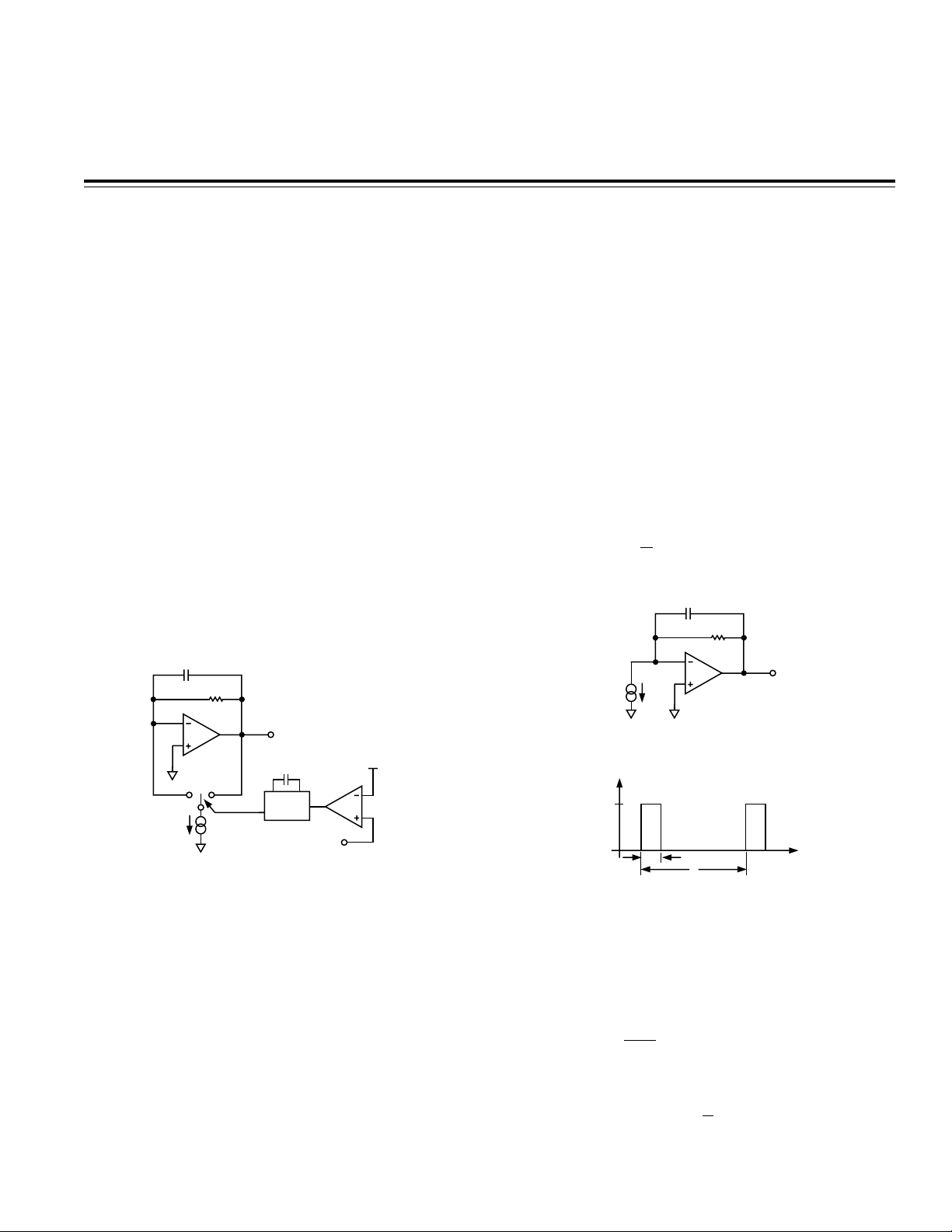
F/V CIRCUIT ARCHITECTURE

Figure 1 shows the major components of the frequency­to-voltage (F/V) converter. It includes a comparator, a
one-shot with a switch, a constant current source, and a
lossy integrator. When the input signal crosses the

C

INT

R

INT

V

OUT

COMP

f

IN

–0.6V

C

OS

ONE

SHOT

␣

Figure 1. Circuit Architecture

threshold at the comparator input, the comparator
triggers the one-shot. The one-shot controls a single
pole double throw switch which directs the current
source to either the summing junction, or the output, of
the lossy integrator. When the one-shot is in its “on”
state, there is current injected into the input of the
integrator and its output rises. When the one-shot
period has passed, the current is steered to the output of
the integrator. Since the output is a low impedance
node, the current has no effect on the circuit and is
effectively turned off. During this time the output falls
due to the discharge of C

through R

INT

. When constant

INT

triggering is applied to the comparator, the integration
capacitor will charge to a relatively steady value and be

REV. B

maintained by constant charging and discharging. The
charge stored on C

is unaffected by loading

INT

because of the low output impedance of the op amp.

THEORY OF OPERATION

Figure 2 shows a simplified representation of the AD650
in the F/V mode. Figure 3 represents the current i(t)
delivered to the lossy integrator. The current can be
thought of as a series of charge packets delivered at

1

f

=

OS

IN

with constant amplitude (α) and

T

)

C

INT

R

INT

V

OUT

i(t)

␣

frequency

duration (t

Figure 2. Simplified Schematic

i(t)

␣

t

OS

T

t

Figure 3. Current i(t) into Integrator

From inspection of Figure 3, the average value of input
current is found by dividing the area of the current i(t) by
the period T. The dc component of the output voltage is
found by scaling the average input current by the
feedback resistor R

V

OUTAVG

=×α.

.

INT

t

OS

R

T

INT

(1a)

Equation 1a becomes a linear function of frequency

when f

is substituted for

IN

VtRf

OUTAVG OS INT IN

=× ××α

1

.

T

(1b)

AN-279

Notice that the relationship between the average output
voltage and input frequency is a function of the one-shot
time constant and the feedback resistor but not of the
integration capacitor. This is because the integration
capacitor is an open circuit to dc. From Equation 1b it is
clear that the most practical way to trim the full-scale
voltage is to include a trim potentiometer in series with
R

. Typically, a 30% trim range will be required to

INT

absorb errors associated with t

and α.

OS

It is also important to characterize the transient
response of the integrator in order to determine settling
time of the F/V to a step change of input frequency. The
transfer function of the lossy integrator is given in the
frequency domain by:

1

VS

()

OUT

IS

()

IN

=

C

INT

S

+

RC

INT INT

1

(2)

×

which indicates that the natural or step response to a
change of input frequency is governed by an
exponential function with time constant π = R

INT

× C

INT.

With the average output voltage and transient response
known, the peak-peak output ripple can be determined
using Equation 3. Once this is determined, a design
algorithm can be developed (Reference 1).

The peak-peak ripple is given by:

//

tRC

()−()

OS OS

eee

V

=

PP

TIRC

−+ −

1

−

e

TIRC

Tt RC

1

××

α

R

(3)

where:

t

= one-shot time constant [seconds]

OS

T

= period of input frequency (1/fIN) [hertz]

R

= integration resistor [ohms]

C

= integration capacitor [farads]

α = current source value (1 mA for AD650) [amps]

Equation 3 accurately represents the ripple amplitude
for a given design. The following section shows how
this equation is used as an iterative part of the total
solution. Equation 3 can also be used to illustrate how
the ripple amplitude changes as a function of input
frequency. It is interesting to note that the ripple
amplitude changes only moderately with input
frequency and has its largest magnitude at the
minimum frequency.

DESIGN PROCEDURE

Recall from looking at Figure 3, that the one-shot “on”
time will be some fraction of the total input period. This
is the time that the circuit integrates the current signal α.
The output ripple can be minimized by allowing the
current source to be on during the majority of this
period. This is achieved by choosing the one-shot time
constant so that it occupies almost the full period of the
input signal when this period is at its minimum (or the
input frequency at its maximum). To design safely and
allow for component tolerance at f

, make t

MAX

OS

approximately equal to 90% of the minimum period.
Given t
C

OS

, the value of the one-shot timing capacitor,

OS

, is determined from Equation 1 in the AD650 data
sheet. This equation has been rearranged and appears
here as:

−

t sec

−×

C

where

(NOTE: For maximum linearity performance use a low dielectric absorp­tion capacitor for COS.)

OS

=

OS

t

OS

×

6.8 10

is in seconds and

7

3

10

3

sec F

/

C

is in farads.

OS

(4)

Once COS is known, the integration resistor is uniquely
determined from the full-scale equation (Equation 1b),
since t

, α, fIN, and V

OS

are known. This leaves only the

OUT

integration capacitor as the final unknown.

C

is chosen by first determining the response time of

INT

the device being measured. If, for example the
frequency signal to be measured is derived from a
mechanical device such as an aircraft turbine shaft, the
momentum of the shaft and the blades should be used
to determine the response time. The time constant of
the F/V is then set to match the time constant of the
mechanical system. It may be set somewhat lower,
depending on the desired total response time of the
mechanical and electrical system. Remember to allow
several time constants (N) for the F/V to approach its
final value. For the first iteration of C

use the following

INT

expression:

C

Mechanical sponse Time

=

INT

Re

×

NR

INT

(5)

where N is the number of time constants chosen to
allow adequate settling. Table I may be used to
determine the number of time constants required for
given settling accuracy.

–2–

REV. B

AN-279

DETERMINE VARIABLES: f

MIN

, f

MAX

RESPONSE TIME , FULL-SCALE
VOLTAGE, MAXIMUM ACCEPTABLE RIPPLE.

CALCULATE:
tOS = 0.9/f

MAX

FIND COS GIVEN t

OS

USING

EQUATION 4.

FIND R

INT

GIVEN V FULL-SCALE

AND t

OS

USING EQUATION 1b.

DETERMINE N BY SYSTEM ACCURACY

USING TABLE I (DEFAULT TO 6 IF UNSURE).

FIND C

INT

USING EQUATION 5.

DECREASE N TO

TRADE RESPONSE

TIME

FOR RIPPLE

CALCULATE RIPPLE USING EQUATION 3

AND f

MIN

.

RIPPLE

TOO

LARGE?

C

INT

IS KNOWN.

DESIGN

COMPLETE.

YES

NO

Table I. Settling Accuracy vs. Number of Time Constants

# of Time
Constants
(N) # of Bits % Accuracy

4.16 6 1.6

4.85 7 0.8

5.55 8 0.4

6.23 9 0.2

6.93 10 0.1

7.62 11 0.05

8.30 12 0.024

9.00 13 0.012

9.70 14 0.006

10.4 15 0.003

11.0 16 0.0015

A larger number of time constants will give a more
responsive circuit but will also increase the ripple at the
F/V output. A practical approach is to start with 8-bit
settling accuracy, using N = 6 time constants, and
increase or decrease N depending on ripple content.

The ripple content is calculated using Equation 3.
Remember that the ripple amplitude will change with
frequency and will be largest at the lowest frequency. It
is also important to note that while in some cases the
ripple amplitude may be large, the average value of the
output voltage will always represent the input frequency
(unless the ripple gets too close and “clips” at the
positive supply rail). Figure 4 shows an example of how
output ripple amplitude will change with input
frequency for a typical application. This graph was
obtained by plotting Equation 3 over the full range of
input frequencies. For design purposes it is only
necessary to calculate ripple at the worst case frequency
(f

). Figure 5 summarizes the design procedure.

MIN

DESIGN EXAMPLE

The rpm of an automobile’s engine is to be monitored
for use by an on-board computer. The rpm signal that
will be generated from an F/V converter is to be digitized
with an 8-bit A/D converter. The rpm range of the engine
extends from 300 rpm to 7000 rpm. A 200-tooth flywheel
at these rotational speeds will generate pulses from
1 kHz up to 23 kHz. The response time to a step change
in throttle position of the engine has been measured, in
neutral, to be 400 ms. The goal is to design an F/V
converter that will respond at approximately the same
rate as the engine, or faster, and will have ripple that is
undetectable by the A/D converter. The A/D converter
has a 10-volt full scale.

1. Let t

be 0.9 × 1/f

OS

= 0.9 × 43.5 µs = 39 µs.

MAX

2. Find COS = 0.0057 µF (from Equation 4) (an impractical
value for polystyrene, but tantalum may be used with
reduced linearity).

V

3.

R

=

INT

mA s kHz

13923

10

××

=

11.14µΩ

k

(from

Equation 1b).

0.015

0.011

– p-p

0.008

OUT

V

0.004

0.000
1000 6500

Figure 4. P-P Ripple vs. Frequency (See Design
Example)

REV. B

RIPPLE VS. FREQUENCY

12000 17500 23000

f

IN

Figure 5. Design Flowchart

–3–

AN-279

(If R

, the load seen by the amplifier, is less than

INT

1kΩ, then t

4. From Table I, an RC network can settle to eight bits in
six time constants so:

C

=

INT

5. Ripple = 6.25 mV @ 300 rpm and 0.67 mV @ 7000 rpm
(from Equation 3).

6. 1/2 LSB size for an 8-bit converter with 10 V full scale
is 19.5 mV. Fortunately, the ripple is below the
quantization level on the first iteration. If desired, the
integration capacitor may be lowered to reduce
response time of the F/V converter.

7. Guessing C
program gives a maximum ripple content of 12.5 mV
and a response time of 200 ms.

THE TRADE-OFF BETWEEN RIPPLE AND RESPONSE
TIME

In many instances some compromise must be made
between ripple and response time. If response time is of
primary importance, the integration capacitor may be
lowered at the expense of increased ripple. Similarly, if
ripple is paramount, the integration capacitor must be
increased resulting in slower response. The design
procedure outlined above assumes that ripple content is
the less desirable effect. Rather than increasing C
low-pass filter could be used, but this also slows the
response time. An approximation to determine total
response time of two cascaded systems, each with
separate response times, can be found by using the
“root sum of squares” technique.

TTT

TOTAL A B

This leads to the “three-to-one” rule, i.e., if TA is more
than three times T
be ignored, hence, T
system.

must be reevaluated.)

OS

ms

40610

1146. Ω

(

)

INT

=+

=

F

µ

.

k

= 3.0 µF or using an iterative computer

22

and their squares are added, TB may

B

is the total response time of the

A

INT

, a

SUMMARY

Low cost voltage-to-frequency converters can be used in
the frequency-to-voltage mode. Trade-offs exist
between output settling time and ripple with the
selection being application-specific. However, by using
the design guidelines highlighted in this note, optimized
performance can be achieved in many applications.

References

1

McGillem, C. D., and G. R. Cooper,

Discrete Signal and System Analysis

Continuous and

, Second Edition.

New York: CBS College Publishing, 1984.

2

Analog Devices Inc. AD650 Data Sheet. Latest version

can be found on www.analog.com.

15.5mV

200␮s

100

0%

⌬

V1

90

10

5mV

Figure 6. Typical Ripple Output

100.10ms

t1.70V

20ms

100

0%

A1

90

10

1V

⌬

Figure 7. Response to Step Change in Frequency

E01373–0–9/00 (rev. B)

–4–

PRINTED IN U.S.A.

REV. B