Analog Devices ADP3811AR, ADP3810AR-8.4, ADP3810AR-4.2, ADP3810AR-16.8, ADP3810AR-12.6 Datasheet

Secondary Side, Off-Line

a

FEATURES
Programmable Charge Current
High Precision Battery Voltage Limit
Precision 2.000 V Reference
Low Voltage Drop Current Sense: 300 mV Full Scale
Full Operation in Shorted and Open Battery Conditions
Drives Diode-Side of Optocoupler
Wide Operating Supply Range: 2.7 V to 16 V
Undervoltage Lockout
SO-8 Package
ADP3810

Internal Precision Voltage Divider for Battery Sense
Four Final Battery Voltage Options Available: 4.2 V,

8.4 V, 12.6 V, 16.8 V

ADP3811

Adjustable Final Battery Voltage

APPLICATIONS
Battery Charger Controller for:

LiIon Batteries (ADP3810)
NiCad, NiMH Batteries (ADP3811)

GENERAL DESCRIPTION

The ADP3810 and ADP3811 combine a programmable current
limit with a battery voltage limit to provide a constant current,
constant voltage battery charger controller. In secondary side,

Battery Charger Controllers

ADP3810/ADP3811

off-line applications, the output directly drives the diode side of
an optocoupler to give isolated feedback control of a primary
side PWM. The circuitry includes two gain (g
sion 2.0 V reference, a control input buffer, an Undervoltage
Lock Out (UVLO) comparator, an output buffer and an over­voltage comparator.

The current limit amplifier senses the voltage drop across an
external sense resistor to control the average current for charg­ing a battery. The voltage drop can be adjusted from 25 mV
to 300 mV, giving a charging current limit from 100 mA to

1.2 amps with a 0.25 Ω sense resistor. An external dc voltage
on the V

input sets the voltage drop. Because this input

CTRL

is high impedance, a filtered PWM output can be used to set
the voltage.

As the battery voltage approaches its voltage limit, the voltage
sense amplifier takes over to maintain a constant battery volt­age. The two amplifiers essentially operate in an “OR” fash­ion. Either the current is limited, or the voltage is limited.

The ADP3810 has internal thin-film resistors that are trimmed
to provide a precise final voltage for LiIon batteries. Four volt­age options are available, corresponding to 1-4 LiIon cells as
follows: 4.2 V, 8.4 V, 12.6 V and 16.8 V.

The ADP3811 omits these resistors allowing any battery volt­age to be programmed with external resistors.

) stages, a preci-

m

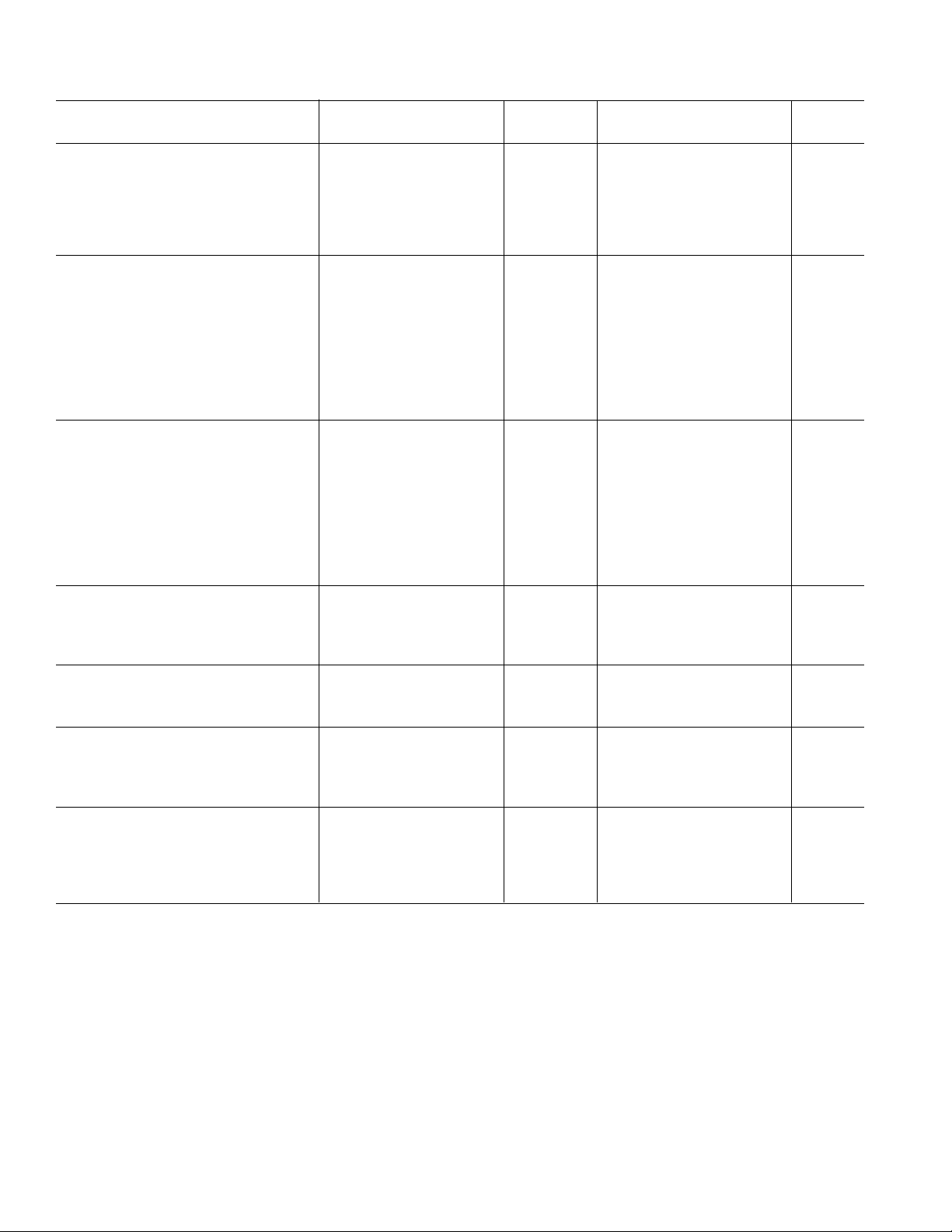
FUNCTIONAL BLOCK DIAGRAM

UVLO

GM

V

CS

GM1

V

CTRL

V

REF

GND

1.5MΩ 80kΩ

OUT

REV. 0

Information furnished by Analog Devices is believed to be accurate and
reliable. However, no responsibility is assumed by Analog Devices for its
use, nor for any infringements of patents or other rights of third parties
which may result from its use. No license is granted by implication or
otherwise under any patent or patent rights of Analog Devices.

V

V

CC

UVLO

UVLO

ADP3810/

ADP3811

One Technology Way, P.O. Box 9106, Norwood, MA 02062-9106, U.S.A.
Tel: [phone] World Wide Web Site: http://www.analog.com
Fax: [phone] © Analog Devices, Inc., 1996

V

SENSE

REF

ADP3810

R1

V

REF

ONLY

R2

GM2

COMP

ADP3810/ADP3811–SPECIFICATIONS

(–408C ≤ TA ≤ +858C, VCC = 10.0 V, unless otherwise noted)

ADP3810

Parameter Conditions Symbol Min Typ Max Units

CURRENT SENSE

Full-Scale Current Sense Voltage V
Minimum Current Sense Voltage 0.0 V ≤ V
Current Programming Input Range V
Gain (V

OUT/VCS

Control Input Bias Current V

VOLTAGE SENSE

Accuracy

2

—ADP3810 –1.0 +1.0 %
Input Resistance—ADP3810 4.2 V Option R
Input Resistance—ADP3810 8.4 V Option R
Input Resistance—ADP3810 12.6 V Option R
Input Resistance—ADP3810 16.8 V Option R
Offset Voltage—ADP3811 V
Bias Current—ADP3811 I
Gain (V

OUT/VSENSE

REFERENCE

Output Voltage C

1

= 1.2 V –315 –300 –285 mV

CTRL

)R

3

)

= 1 kΩ A

L

Pin I

CTRL

R

= 1 kΩ A

L

= 0.1 µF

L

≤ 0.1 V –32 –25 –18 mV

CTRL

4

CTRL
VCS

BCTRL

IN
IN
IN
IN
OS

B

VBAT

V

REF

0.0 1.2 V
74 86 dB

10 40 nA

210k Ω
420k Ω
630k Ω
840k Ω

–2.5 +2.5 mV

110 nA

60 74 dB

2.000 V

Accuracy

ADP3810 –1.0 +1.0 %

ADP3811 –1.8 +1.8 %
Load Regulation I
Line Regulation V
Output Voltage Noise 0.1 Hz to 10 Hz e
Load Current (Sourcing) I

= 0 mA to 5 mA –0.25 +0.25 %

LOAD

= 2.7 V to 16 V 0.004 0.02 %/V

CC

N

L

510 mA

35 µV p-p

OUTPUT

Output Current V
Saturation Voltage I
Gain (V

OUT/VCOMP

)R

= 2.7 V I

CC

= 4 mA, VCC–V

OUT

= 1 kΩ A

L

OUT

OUT

V

SAT
VOUT

46 mA

0.1 0.4 V
6 V/V

UNDERVOLTAGE LOCKOUT

Trip Point-On 2.65 2.7 V
Trip Point-Off 2.5 2.6 V

POWER SUPPLY

Operating Range 2.7 16 V
Quiescent Current V
Turn-Off Current V

≥ 2.7 V I

CC

≤ 2.5 V 0.5 1 mA

CC

Q

1.5 3 mA

OVERVOLTAGE COMPARATOR

Threshold

ADP3810 Percent Above Full Scale

ADP3811 Percent Above Full Scale
Response Time I

NOTES

1

20 kΩ resistor from current sense voltage to V

2

Applies to 4.2 V, 8.4 V, 12.6 V and 16.8 V options. Includes all error from offset voltage, bias current, resistor divider and voltage reference.

3

Does not include attenuation of input resistor divider for ADP3810.

4

0.1 µF load capacitor required for reference operation.

5

Full scale is the programmed final battery voltage: 4.2 V, 8.4 V, 12.6 V or 16.8 V for the ADP3810 or 2.0 V at V

All limits at temperature extremes are guaranteed via correlation using standard Statistical Quality Control (SQC) methods.
Specifications subject to change without notice.

CS

pin.

from 0 mA to 2 mA t

OUT

5

VOV%6%

5

VOV%6%

r

for the ADP3811.

SENSE

8 µs

–2–

REV. 0

ADP3810/ADP3811

ABSOLUTE MAXIMUM RATINGS

Supply Voltage, VCC . . . . . . . . . . . . . . . . . . . –0.4 V to 18 V

V

, VCS Input Range . . . . . . . . . . . . . . . . . . –0.4 V to V

CTRL

V

Input Range (ADP3811) . . . . . . . . . . . . –0.4 V to V

SENSE

V

Input Range (ADP3810) . . . . . . . . . . . –0.4 V to 20 V

SENSE

CC
CC

Maximum Power Dissipation . . . . . . . . . . . . . . . . . . 500 mW

Operating Temperature Range . . . . . . . . . . . –40°C to +85°C

Storage Temperature Range . . . . . . . . . . . . . –65°C to 150°C

Lead Temperature (Soldering, 10 sec) . . . . . . . . . . . .+300°C

ORDERING GUIDE

Temperature Package Battery

Model Range Option Voltage

ADP3810AR-4.2 –40°C to +85°C SO-8 4.2 V

ADP3810AR-8.4 –40°C to +85°C SO-8 8.4 V

ADP3810AR-12.6 –40°C to +85°C SO-8 12.6 V

ADP3810AR-16.8 –40°C to +85°C SO-8 16.8 V

ADP3811AR –40°C to +85°C SO-8 Adjustable

OUT

GND

RETURN

V

RCS

R3

0.1µF

IN

CTRL

DC/DC

CONVERTER

V

IN

PIN CONFIGURATION

8

V

SENSE

COMP

V

OUT

CS

1

ADP3810

2

ADP3811

TOP VIEW

3

(Not to Scale)

4

V

CC

7

V

REF

6

GND
V

5

CTRL

PIN DESCRIPTION

Mnemonic Function

V

SENSE

V

CS

V

REF

Battery Voltage Sense Input.
Current Sense Input.

Reference Output. Nominally 2.0 V.
COMP External Compensation Pin.
OUT Optocoupler Current Output Drive.
V
V

CTRL

CC

DC Control Input to Set Current Limit, 0 V to 1.2 V.

Positive Supply.
GND Ground Pin.

V

BAT

I

R1

R2

CHARGE

ADP3811

ONLY

R

CS

2.0V

0.1µF

BATTERY

V

V

REF

1.5MΩ

V

CTRL

BUFFER

I

OUT

OUT

CS

80kΩ

GM1

UVLO

GM3

200Ω

1.2V

V

CC

UVLO

UVLO

ADP3810/

ADP3811

COMP

REF

GND

V

R1

GM2

SENSE

ADP3810

R2

ONLY

V

V

REF

100µA

C

C

R

C

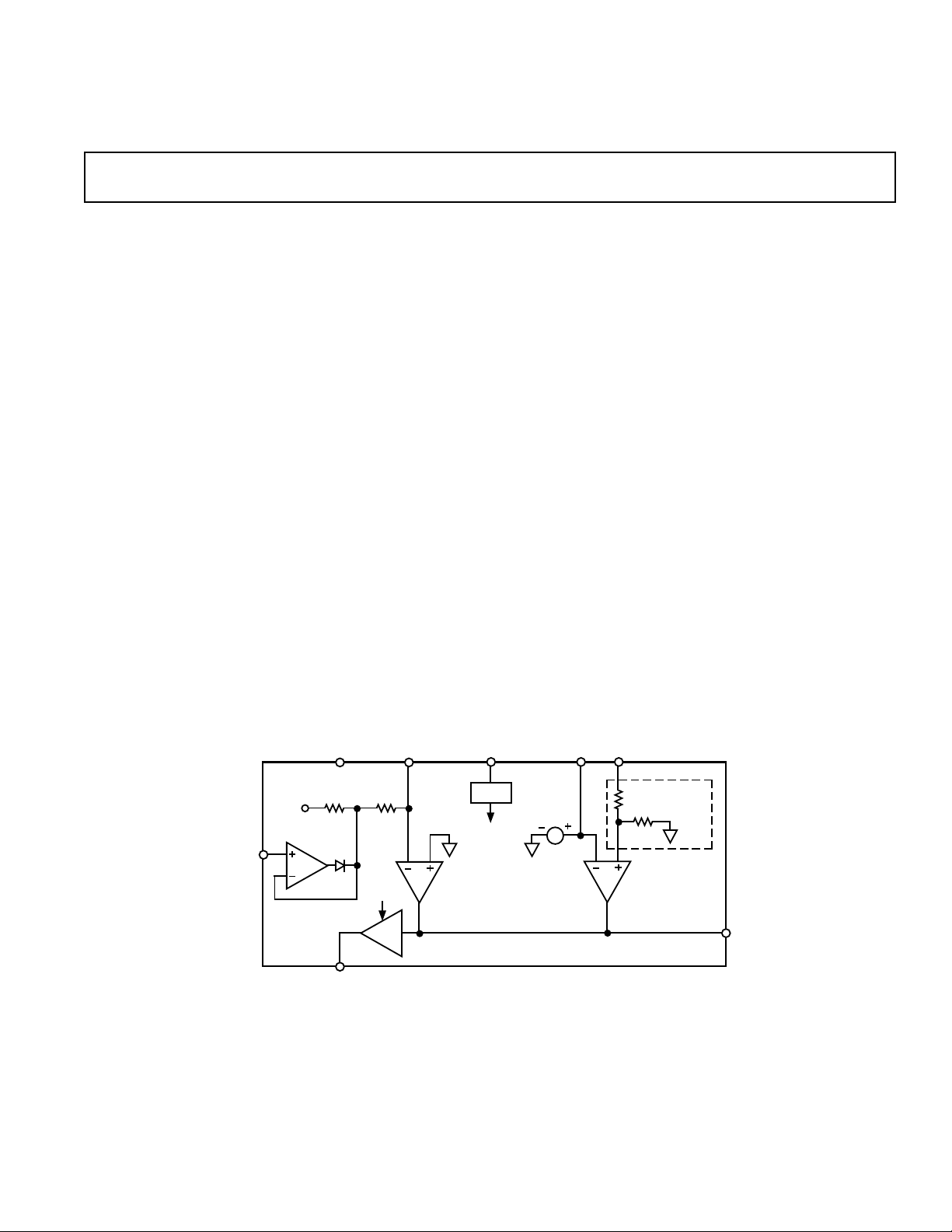
Figure 1. Simplified Battery Charger

CAUTION

ESD (electrostatic discharge) sensitive device. Electrostatic charges as high as 4000 V readily
accumulate on the human body and test equipment and can discharge without detection.
Although the ADP3810/ADP3811 features proprietary ESD protection circuitry, permanent
damage may occur on devices subjected to high energy electrostatic discharges. Therefore, proper
ESD precautions are recommended to avoid performance degradation or loss of functionality.

WARNING!

ESD SENSITIVE DEVICE

REV. 0

–3–

ADP3810/ADP3811

TEMPERATURE – °C

REFERENCE DROPOUT VOLTAGE – Volts

0.12

0.04
–50 –25 100

0255075

0.10

0.08

0.06

0.14

V

CC

= +10V

I

L

= 5mA

C

L

= 0.1µF

CONTROL VOLTAGE, V

CTRL

– Volts

CHARGE CURRENT – Amps

1.6

1.4

0

0 0.2 1.4

0.4 0.6 0.8 1.0

1.2

1.0

0.2

0.8

0.6

0.4

1.2

RCS = 0.25Ω
R3 = 20kΩ

–Typical Performance Characteristics

2.004
2 TYPICAL PARTS

2.002

2.000

1.998

1.996

REFERENCE VOLTAGE – Volts

1.994

–50 –25 100

0255075

TEMPERATURE – °C

V

CC

I

= 100µA

L

C

L

= +10V

= 0.1µF

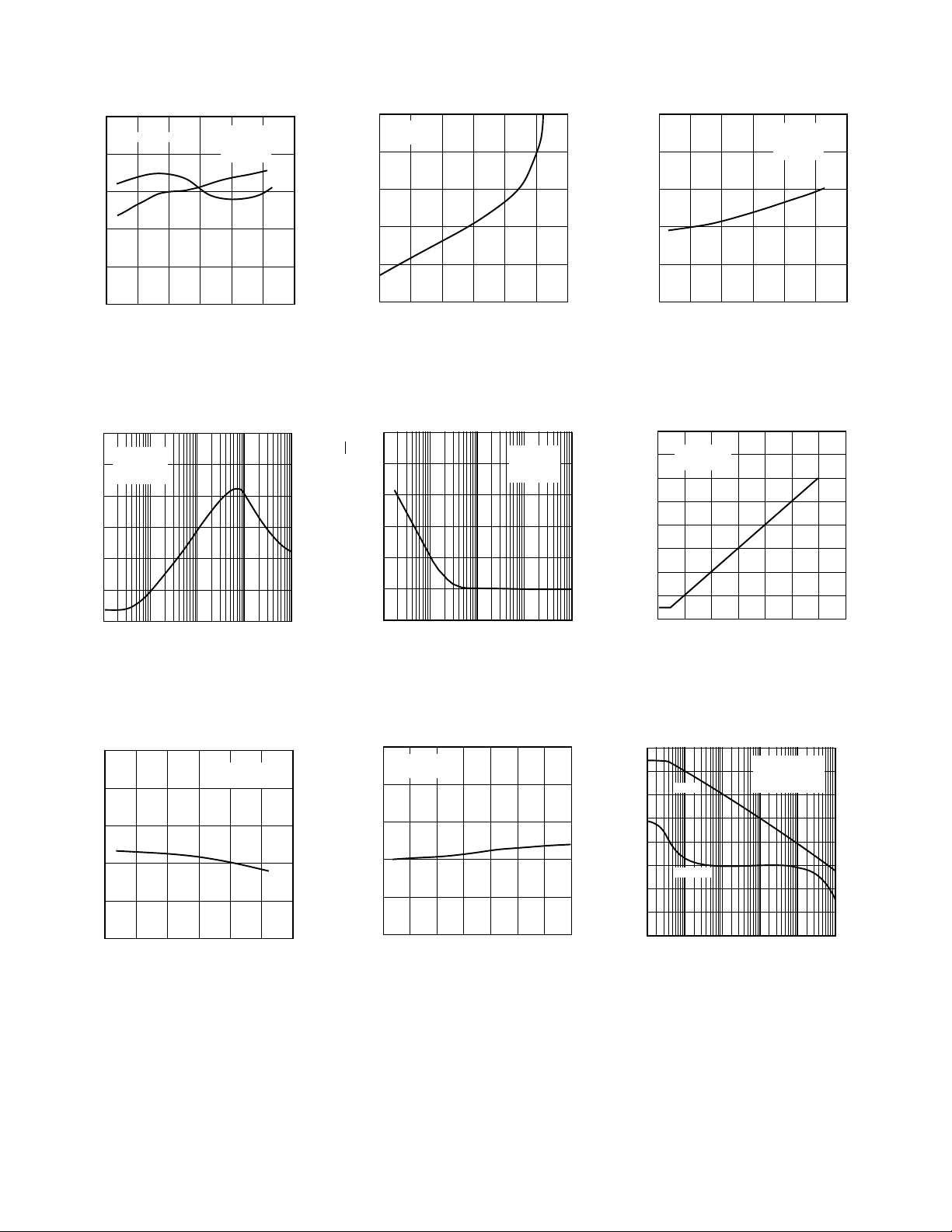
Figure 2. Reference Output Voltage
vs. Temperature for Two Typical Parts

–20

V

= +10V

CC

I

= 100µA

–30

L

C

= 0.1µF

L

–40

–50

PSRR – dB

–60

250

V

= +10V

CC

C

= 0.1µF

L

200

150

100

50

DROPOUT VOLTAGE – mV

0

03 18

6 9 12 15

LOAD CURRENT – mA

Figure 3. Reference Drop-Out Volt
age (V

3000

Hz

√

2500

2000

1500

1000

) vs. Load Current

CC–VREF

V

= +10V

CC

I

= 100µA

L

CL = 0.1µF

Figure 4. Reference Dropout Voltage
vs. Temperature

–70

–80

100 1k 1M

FREQUENCY – Hz

Figure 5. Reference PSRR vs.
Frequency

–294

–296

–298

–300

–302

CURRENT SENSE VOLTAGE – mV

–304

–50 –25 100

Figure 8. Full-Scale Current Sense
Voltage vs. Temperature

0255075

TEMPERATURE – °C

10k 100k

VCC = +10V
R3 = 20kΩ

500

REFERENCE NOISE DENSITY – nV/

0

1 10 10k

100 1k

FREQUENCY – Hz

Figure 6. Reference Noise Density
vs. Frequency

–294

V

= +10V

CC

R3 = 20kΩ

–296

–298

–300

–302

CURRENT SENSE VOLTAGE – mV

–304

24 16

6 8 10 12 14

SUPPLY VOLTAGE, VCC – Volts

Figure 9. Full-Scale Current Sense
Voltage vs. V

CC

–4–

Figure 7. Charge Current vs. Control
Voltage

100

80

GAIN

60

40

20

0

PHASE

–20

OPEN-LOOP GAIN – dB

–40

–60

100 1k

10 1M10k

FREQUENCY – Hz

C
T
V

COMP
A
CC

= 0.01µF

= +25°C

= +10V

100k

0

45

90

135

180

225

Figure 10. GM1 Open-Loop Gain and
Phase vs. Frequency

REV. 0

PHASE SHIFT – Degrees

ADP3810/ADP3811

SUPPLY VOLTAGE, VCC – Volts

1.0

0.5

–1.5

03 18

6 9 12 15

0

–0.5

–1.0

VOLTAGE SENSE ACCURACY – %

TA = +25°C

TEMPERATURE – °C

V

SENSE

BIAS CURRENT – nA

2.5

2.0

0

–50 –25 100

0255075

1.5

1.0

0.5

VCC = +10V

TEMPERATURE – °C

V

OV%

– %

12

10

2

–50 –25 100

0255075

8

6

4

VCC = +10V

100

80

GAIN

60

40

20

0

PHASE

–20

OPEN-LOOP GAIN – dB

–40

–60

100 1k

10 1M10k

FREQUENCY – Hz

C
T

A

V

CC

COMP

= +25°C

= +10V

= 0.01µF

100k

0

45

90

135

180

225

Figure 11. GM2 Open-Loop Gain and
Phase vs. Frequency

1.0

0.5

0

–0.5

GM2 OFFSET – mV

–1.0

VCC = +10V

1.0
V

= +10V

CC

0.5

0

–0.5

–1.0

VOLTAGE SENSE ACCURACY – %

PHASE SHIFT – Degrees

–1.5

–50 –25 1000 255075

TEMPERATURE – °C

Figure 12. ADP3810 Voltage Sense
Accuracy vs. Temperature

1.0

TA = +25°C

0.5

0

–0.5

GM2 OFFSET – mV

–1.0

Figure 13. ADP3810 Voltage Sense
Accuracy vs. V

CC

–1.5

–50 –25 100

0255075

TEMPERATURE – °C

Figure 14. ADP3811 GM2 Offset vs.
Temperature

2.5

2.0

1.5

1.0

BIAS CURRENT – nA

SENSE

0.5

V

0

03 18

6 9 12 15

SUPPLY VOLTAGE, VCC – Volts

Figure 17. ADP3811 V
Current vs. V

CC

TA = +25°C

Bias

SENSE

–1.5

03 18

6 9 12 15

SUPPLY VOLTAGE, VCC – Volts

Figure 15. ADP3811, GM2 Offset
vs. V

CC

120

V

= +10V

CC

T

= +25°C

A

100

80

60

40

QUANTITY – Parts

20

0

5.0 5.2 5.4 5.6 5.8 6.0 6.2 6.4 6.6 6.8 7.0
V

– %

OV%

Figure 18. Overvoltage Comparator
Distribution (V

OV%

)

Figure 16. ADP3811 V

SENSE

Bias

Current vs. Temperature

Figure 19. Overvoltage Comparator
Threshold (V

vs. Temperature

OV%)

REV. 0

–5–

ADP3810/ADP3811

TEMPERATURE – °C

0.25

0.20

0
–50 –25 100

0255075

0.15

0.10

0.05

OUTPUT SATURATION

VOLTAGE, V

SAT

– Volts

V

CC

= +10V

I

LOAD

= 5mA

240

V

= +10V

CC

T

= +25°C

A

200

= 1kΩ

R

L

160

120

80

QUANTITY – Parts

40

0

5.0 5.2 5.4 5.6 5.8 6.0 6.2 6.4 6.6 6.8 7.0
OUTPUT GAIN (V

OUT/VCOMP

Figure 20. Output Gain (V
Distribution

) – V/V

OUT/VCOMP

)

– V/V

COMP

/V

OUT

V

Figure 21. Output Gain (V
vs. V

APPLICATIONS SECTION
Functional Description

The ADP3810 and ADP3811 are designed for charging NiCad,
NiMH and LiIon batteries. Both parts provide accurate voltage
sense and current sense circuitry to control the charge current
and final battery voltage. Figure 1 shows a simplified battery
charging circuit with the ADP3810/ADP3811 controlling an
external dc-dc converter. The converter can be one of many
different types such as a Buck converter, Flyback converter or a
linear regulator. In all cases, the ADP3810/ADP3811 maintains
accurate control of the current and voltage loops, enabling the
use of a low cost, industry standard dc-dc converter without
compromising system performance. Detailed realizations of
complete circuits including the dc-dc converter are included
later in this data sheet.

The ADP3810 and ADP3811 contain the following blocks
(shown in Figure 1):

• Two “GM” type error amplifiers control the current loop
(GM1) and the voltage loop (GM2).

• A common COMP node is shared by both GM amplifiers
such that an RC network at this node helps compensate both
control loops.

• A precision 2.0 V reference is used internally and is available
externally for use by other circuitry. The 0.1 µF bypass ca-
pacitor shown is required for stability.

• A current limited buffer stage (GM3) provides a current out­put, I

, to control an external dc-dc converter. This out-

OUT

put can directly drive an optocoupler in isolated converter
applications. The dc-dc converter must have a control scheme
such that higher I

results in lower duty cycle. If this is

OUT

not the case, a simple, single transistor inverter can be used
for control phase inversion.

• An amplifier buffers the charge current programming volt­age, V

• An UVLO circuit shuts down the GM amplifiers and the
output when the supply voltage (V
protects the charging system from indeterminate operation.

• A transient overshoot comparator quickly increases I
when the voltage on the “+” input of GM2 rises over 120 mV
above V
quickly recover from overvoltage transients and protect ex-

, to provide a high impedance input.

CTRL

) falls below 2.7 V. This

CC

. This clamp shuts down the dc-dc converter to

REF

ternal circuitry.

8

RL = 1kΩ
V

= +1.0V

OUT

7

TA = –40°C

6

5

4

3

CC

TA = +85°C

03 18

6 9 12 15

TA = +25°C

VCC – Volts

OUT/VCOMP

Description of Battery Charging Operation

The IC based system shown in Figure 1 charges a battery with a
dc current supplied by a dc-dc converter, which is most likely a
switching type supply but could also be a linear supply where
feasible. The value of the charge current is controlled by the
feedback loop comprised of R
converter and a dc voltage at the V
charge current is set by the voltage, V
upon the choice for the values of R
formula below:

Typical values are R
in a charge current of 1.0 A for a control voltage of 1.0 V. The
80 kΩ resistor is internal to the IC, and it is trimmed to its ab­solute value. The positive input of GM1 is referenced to
ground, forcing the V

The resistor R
V

, and it is this voltage that GM1 is regulating. The voltage

RCS

at V

RCS

1.0 V, V

CS

is equal to –(R3/80 kΩ) V

equals –250 mV. If V

RCS

grammed level (i.e., the charge current increases), the negative
input of GM1 goes slightly below ground. This causes the out­put of GM1 to source more current and drive the COMP node
high, which forces the current, I
decreases the drive to the dc-dc converter, reducing the charg­ing current and balancing the feedback loop.

As the battery approaches its final charge voltage, the voltage
loop takes over. The system becomes a voltage source, floating
the battery at constant voltage thereby preventing overcharging.
The constant voltage feature also protects the circuitry that is
actually powered by the battery from overvoltage if the battery is
removed. The voltage loop is comprised of R1, R2, GM2 and
the dc-dc converter. The final battery voltage is simply set by
the ratio of R1 and R2 according to the following equation
(V

= 2.000 V):

REF

OUT

If the battery voltage rises above its programmed voltage,
V

is pulled above V

SENSE

current, raising the COMP node voltage and I

–6–

)

I

CHARGE

Figure 22. V

, R3, GM1, the external dc-dc

CS

CTRL

CS

1

=

= 0.25 Ω and R3 = 20 kΩ, which result

CS

pin to a virtual ground.

CS

R3

×

R

80 kΩ

CS

vs. Temperature

SAT

input. The actual

, and is dependent

CTRL

and R3 according to the

×V

CTRL

converts the charge current into the voltage at

V

BAT

. When V

CTRL

falls below its pro-

RCS

, to increase. A higher I

OUT





=2.000V ×

. This causes GM2 to source more

REF

R1

+1





R2





equals

CTRL

. As with the

OUT

OUT

REV. 0

ADP3810/ADP3811

current loop, the higher I

reduces the duty cycle of the dc-dc

OUT

converter and causes the battery voltage to fall, balancing the
feedback loop.

Each GM stage is designed to be asymmetrical so that each am­plifier can only source current. The outputs are tied together at
the COMP node and loaded with an internal constant current
sink of approximately 100 µA. Whichever amplifier sources
more current controls the voltage at the COMP node and there­fore controls the feedback. This scheme is a realization of an
analog “OR” function where GM1 or GM2 has control of the
dc-dc converter and the charging circuitry. Whenever the cir­cuit is in full current limiting or full voltage limiting, the respec­tive GM stage sources an identical amount of current to the
fixed current sink. The other GM stage sources zero current
and is out of the loop. In the transition region, both GM stages
source some of the current to comprise the full amount of the
current sink. The high gains of GM1 and GM2 ensure a
smooth but sharp transition from current control to voltage con­trol. Figure 24 shows a graph of the transition from current to
voltage mode, that was measured on the circuit in Figure 23 as
detailed below. Notice that the current stays at its full pro­grammed level until the battery is within 200 mV of the final pro­grammed voltage (10 V in this case), which maintains fast
charging through almost all of the battery voltage range. This
improves the speed of charging compared to a scheme that re­duces the current at lower battery voltages.

The second element in a battery charging system is some form
of a dc-dc converter. To achieve high efficiency, the dc-dc con­verter can be an isolated off-line switching power supply, or it
can be an isolated or nonisolated Buck or other type of switch­ing power supply. For lower efficiency requirements, a linear
regulator fed from a wall adapter can be used. In the above dis­cussion, the current, I
supply; but in the case of the linear regulator, I

, controls the duty cycle of a switching

OUT

controls the

OUT

pass transistor drive. Examples of these topologies are shown
later in this data sheet. If an off-line supply such as a flyback
converter is used, and isolation between the control logic and
the ADP3810/ADP3811 is required, an optocoupler can be in­serted between the ADP3810/ADP3811 output and the control
input of the primary side PWM.

Charge Termination

If the system is charging a LiIon battery, the main criteria to de­termine charge termination is the absolute battery voltage. The
ADP3810, with its accurate reference and internal resistors, ac­complishes this task. The ADP3810’s guaranteed accuracy
specification of ±1% of the final battery voltage ensures that a
LiIon battery will not be overcharged. This is especially impor­tant with LiIon batteries because overcharging can lead to cata­strophic failure. It is also important to insure that the battery be
charged to a voltage equal to its optimal final voltage (typically

4.2 V per cell). Stopping at less than 1% of full-scale results in
a battery that has not been charged to its full mAh capacity,
reducing the battery’s run time and the end equipment’s operat­ing time.

The ADP3810/ADP3811 does not include circuitry to detect
charge termination criteria such as –∆V/∆t or ∆T/∆t, which are
common for NiCad and NiMH batteries. If such charge termi­nation schemes are required, a low cost microcontroller can be
added to the system to monitor the battery voltage and tempera­ture. A PWM output from the microcontroller can subsequently

program the V
impedance of V

input to set the charge current. The high

CTRL

enables the inclusion of an RC filter to in-

CTRL

tegrate a PWM output into a dc control voltage.

Compensation

The voltage and current loops have significantly different natu­ral and crossover frequencies in a battery charger application, so
the two loops most likely need different pole/zero feedback com­pensation. Figure 1 shows a single RC network from the
COMP node to ground. This is primarily for low frequency
compensation (f

< 100 Hz) of the voltage loop. Since the

C

COMP node is shared by both GM stages, this compensation
also affects the current loop. The internal 200 Ω resistor does
change the zero location of the compensation for the current
loop with respect to the voltage loop. To provide a separate
higher frequency compensation (f

~ 1 kHz–10 kHz), a second

C

series RC may be needed. A detailed calculation of the com­pensation values is given later in this data sheet.

ADP3810 and ADP3811 Differences

The main difference between the ADP3810 and the ADP3811
is illustrated in Figure 1. The resistors R1 and R2 are external
for the ADP3811 and internal for the ADP3810. The ADP3810
is specifically designed for LiIon battery charging, and thus, the
internal resistors are precision thin-film resistors laser trimmed
for LiIon cell voltages. Four different final voltage options are
available in the ADP3810: 4.2 V, 8.4 V, 12.6 V, and 16.8 V.
For slightly different voltages to accommodate different LiIon
chemistries, please contact the factory. The ADP3811 does not in­clude the internal resistors, allowing the designer to choose any
final battery voltage by appropriately selecting the external resis­tors. Because the ADP3810 is specifically for LiIon batteries,
the reference is trimmed to a tighter accuracy specification of
±1% instead of ±2% for the ADP3811.

V

Input and Charge Current Programming Range

CTRL

The voltage on the V

input determines the charge current

CTRL

level. This input is buffered by an internal single supply ampli­fier (labeled BUFFER) to allow easy programmability of V
For example, for a fixed charge current, V

can be set by a

CTRL

CTRL

.

resistor divider from the reference output. If a microcontroller
is setting the charge current, a simple RC filter on V

CTRL

enables
the voltage to be set by a PWM output from the micro. Of
course, a digital-to-analog converter could also be used, but the
high impedance input makes a PWM output the economical
choice. The bias current of V

is typically 25 nA, which

CTRL

flows out of the pin.
The guaranteed input voltage range of the buffer is from 0.0 V

to 1.2 V. When V

is in the range of 0.0 V to 0.1 V, the out-

CTRL

put of the internal amplifier is fixed at 0.1 V. This corresponds
to a charge current of 100 mA for R
The graph of charge current versus V

= 0.25 Ω, R3 = 20 kΩ.

CS

in Figure 7 shows this

CTRL

relationship. Figure 1 shows a diode in series with the buffer’s
output and a 1.5 MΩ resistor from V

to this output. The

REF

diode prevents the amplifier from sinking current, so for small
input voltages the buffer has an open output. The 1.5 MΩ
resistor forms a divider with the internal 80 kΩ resistor to fix the
output at 0.1 V, i.e., about 10% of the maximum current. This
corresponds to the typical trickle charge current level for NiCad
batteries. When V

rises above 0.1 V, the buffer sources

CTRL

current and the output follows the input. The total range of
V

from 0.0 V. to 1.2 V results in a charge current range

CTRL

from 100 mA to 1.2 A (for R

= 0.25 Ω, R3 = 20 kΩ). Larger

CS

REV. 0

–7–

ADP3810/ADP3811

charge current levels can be obtained by either reducing the
value of R

or increasing the value of R3. The main penalty of

CS

increasing R3 is lower efficiency due to the larger voltage drop
across R

, and the penalty of decreasing RCS is lower accuracy

CS

(but higher efficiency) as discussed below.

V

Output

REF

The internal band gap reference is not only used internally for
the voltage and current loops, but it is also available externally if
an accurate voltage is needed. The reference employs a pnp
output transistor for low dropout operation. Figure 3 shows a
typical graph of dropout voltage versus load current. The refer­ence is guaranteed to source 5 mA with a dropout voltage of
400 mV or less. The 0.1 µF capacitor on the reference pin is in-
tegral in the compensation of the reference and is therefore re­quired for stable operation. If desired, a larger value of capacitance
can also be used for the application, but a smaller value should
not be used. This capacitor should be located close to the V

REF

pin. Additional reference performance graphs are shown in Fig­ures 2 through 6.

Output Stage

The output stage performs two important functions. It is a
buffer for the compensation node, and as such, it has a high im­pedance input. It is also a GM stage. The OUT pin is a current
output to enable the direct drive of an optocoupler for isolated
applications. The gain from the COMP node to the OUT pin is
approximately 5 mA/V. With a load resistor of 1 kΩ, the voltage
gain is equal to five as specified in the data sheet. A different
load resistor results in a gain equal to R

× (5 mA/V). Figures

L

20 and 21 show how the gain varies from part to part and versus
the supply voltage, respectively. The guaranteed output current
is 5 mA, which is much more than the typical 1 mA to 2 mA re­quired in most applications.

Current Loop Accuracy Considerations

The accuracy of the current loop is dependent on several factors
such as the offset of GM1, the offset of the V

buffer, the ra-

CTRL

tio of the internal 80 kΩ compared to the external 20 kΩ resis­tor, and the accuracy of R
accuracy states that the full-scale current sense voltage, V

. The specification for current loop

CS

RCS

, of

–300 mV is guaranteed to be within 15 mV of this value. This
assumes an exact 20 kΩ resistor for R3. Any errors in this resis­tor will result in further errors in the charge current value. For
example, a 5% error in resistor value will add a 5% error to the
charge current. The same is true for R

, the current sense resis-

CS

tor. Thus, 1% or better resistors are recommended.
As mentioned above, decreasing the value of R

charge current. Since it is V
value of R
where R

is not accounted for in the specification. An example

CS

= 0.1 Ω illustrates its impact on the accuracy of the

CS

charge current. The range of V

that is specified, the actual

RCS

is from –25 mV ± 5 mV to

RCS

increases the

CS

–300 mV ± 15 mV. This results in a charge current range from
250 mA ± 50 mA to 3 A ± 150 mA, as opposed to a charge cur­rent range of 100 mA ± 20 mA to 1.2 A ± 60 mA for R

CS

=

0.25 Ω. Thus, not only is the minimum current changed, but
the absolute variation around the set point is increased (although
the percentage variation is the same).

Voltage Loop Accuracy Considerations

The accuracy of the voltage loop is dependent on the offset of
GM2, the accuracy of the reference voltage, the bias current of
GM2 through R1 and R2, and the ratio of R1/R2. For the de­manding application of charging LiIon batteries, the accuracy of

the ADP3810 is specified with respect to the final battery volt­age. This is tested in a full feedback loop so that the single ac­curacy specification given in the specification table accounts for
all of the errors mentioned above. For the ADP3811, the resis­tors are external, so the final voltage accuracy needs to be deter­mined by the designer. Certainly, the tolerance of the resistors
has a large impact on the final voltage accuracy, and 1% or bet­ter is recommended.

Supply Range

The supply range is specified from 2.7 V to 16 V. However, a
final battery voltage option for the ADP3810 is 16.8 V. The

16.8 V is divided down by the thin film resistors to 2.0 V inter­nally. Thus, the input to GM2 never sees much more than 2.0 V,
which is well below the V

voltage limit. In fact, VCC can be

CC

fixed to 2.7 V and the ADP3810 will still control the charging of
a 16.8 V battery stack. The ADP3811, with external resistors,
can charge batteries to voltages well in excess of its supply volt­age. However, if the final battery voltage is above 16 V, V

CC

cannot be supplied directly from the battery as it is in Figure 1.
Alternative circuits must be employed as will be discussed later.
Decoupling capacitors should be located close to the supply pin.
The actual value of the capacitors depends on the application,
but at the very least a 0.1 µF capacitor should be used.

OFF-LINE, ISOLATED, FLYBACK BATTERY CHARGER

The ADP3810 and ADP3811 are ideal for use in isolated charg­ers. Because the output stage can directly drive an optocoupler,
feedback of the control signal across an isolation barrier is a
simple task. Figure 23 shows a complete flyback battery charger
with isolation provided by the flyback transformer and the
optocoupler. The essential operation of the circuit is not much
different from the simplified circuit described in Figure 1. The
GM1 loop controls the charge current, and the GM2 loop con­trols the final battery voltage. The dc-dc converter block is
comprised of a primary side PWM circuit and flyback trans­former, and the control signal passes through the optocoupler.

The circuit in Figure 23 incorporates all of the features neces­sary to assure long battery life with rapid charging capability.
By using the ADP3810 for charging LiIon batteries, or the
ADP3811 for NiCad and NiMH batteries, component count is
minimized, reducing system cost and complexity. With the cir­cuit as presented or with its many possible variations, designers
no longer need to compromise charging performance and bat­tery life to achieve a cost effective system.

Primary Side Considerations

A typical current-mode flyback PWM controller was chosen for
the primary control circuit for several reasons. First and most
importantly, it is capable of operating from very small duty
cycles to near the maximum designed duty cycle. This makes it
a good choice for a wide input ac supply voltage variation re­quirement, which is usually between 70 V–270 V ac for world
wide applications. Add to that the additional requirement of
0% to 100% current control, and the PWM duty cycle must
have a wide range. This charger achieves these ranges while
maintaining stable feedback loops.

The detailed operation and design of the primary side PWM is
widely described in the technical literature and is not detailed
here. However, the following explanation should make clear the
reasons for the primary side component choices. The PWM fre­quency is set to around 100 kHz as a reasonable compromise

–8–

REV. 0

ADP3810/ADP3811

9.1Ω

3W

1A

L

N

AC

120/220V–

22nF

1N4148

13V

330pF

330Ω

10kΩ

10Ω

1kΩ

1.6Ω470pF

47µF

C

F

1nF

R

F

3.3kΩ

3.3kΩ

100kΩ

IRFBC30

50µF/450V

TX1**

10nF

1N4148

100Ω

22µF

C

F1

1mF

R3
20kΩ*

MURD320

R

CS

0.25Ω*

C

C2

0.2µF

R

C2

300Ω

R4

1.2kΩ

3.3V

0.1µF

3.3kΩ

2.2nF

OPTO COUPLER

MOC8103

C

F2

220µF

0.1µF0.1µF

R1

80.6kΩ*

R2
20kΩ*

R

C1

10kΩ

C

C1

1µF

V

CS

V

CC

V

REF

V

SENSE

OUT

COMP

GND

V

CTRL

0.1µF

ADP3810/ADP3811

V

OUT

BATTERY

CHARGE
CURRENT
CONTROL
VOLTAGE

MAXIMUM V

OUT

= +10V

CHARGE CURRENT 0.1A TO 1A

* 1% TOLERANCE
** TX1

f = 120kHz

L

PR

= 750µH

L

SEC

= 7.5µH

V

CC

OUTPUT

COMP

V

FB

I

SENSE

V

REF

RT/CT GND

PWM

3845

Figure 23. ADP3810/ADP3811 Controlling an Off-Line, Flyback Battery Charger

between inductive and capacitive component sizes, switching
losses and cost.

The primary PWM-IC circuit derives its starting V

through a

CC

100 kΩ resistor directly from the rectified ac input. After start­up, a conventional bootstrapped sourcing circuit from an auxil­iary flyback winding wouldn’t work, since the flyback voltage
would be reduced below the minimum V

level specified for

CC

the 3845 under a shorted or discharged battery condition. There­fore, a voltage doubler circuit was developed (as shown in Fig­ure 23) that provides the minimum required V

for the IC

CC

across the specified ac voltage range even with a shorted battery.
While the signal from the ADP3810/ADP3811 controls the av-

erage charge current, the primary side should have a cycle by
cycle limit of the switching current. This current limit has to be
designed so that, with a failed or malfunctioning secondary cir­cuit or optocoupler, the primary power circuit components (the
FET and transformer) won’t be overstressed. In addition, dur­ing start-up or for a shorted battery, V
ADP3811 won’t be present. Thus, the primary side current
limit is the only control of the charge current. As the secondary
side V
and controls the average current. The primary side current limit
is set by the 1.6 Ω current sense resistor connected between the

to the ADP3810/

CC

rises above 2.7 V, the ADP3810/ADP3811 takes over

CC

power NMOS transistor, IRFBC30, and ground.
The current drive of the ADP3810/ADP3811’s output stage di-

rectly connects to the photodiode of an optocoupler with no ad­ditional circuitry. With 5 mA of output current, the output stage
can drive a variety of optocouplers. An MOC8103 is shown as
an example. The current of the photo-transistor flows through
the 3.3 kΩ feedback resistor, R
3845’s COMP pin, thus controlling the PWM duty cycle. The
controlled switching regulator should be designed as shown so
that more LED current from the optocoupler reduces the duty
cycle of the converter. Approximately 1 mA should be the

REV. 0

, setting the voltage at the

FB

maximum current needed to reduce the duty cycle to zero. The
difference between the 5 mA drive and the 1 mA requirement
leaves ample margin for variations in the optocoupler gain.

Secondary Side Considerations

For the lowest cost, a current-mode flyback converter topology
is used. Only a single diode is needed for rectification
(MURD320 in Figure 23), and no filter inductor is required.
The diode also prevents the battery from back driving the
charger when input power is disconnected. A 1 mF capacitor
filters the transformer current, providing an average dc current
to charge the battery. The resistor, R
rent which is controlled via the V

, senses the average cur-

CS

input. In this case, the

CS

charging current has high ripple due to the flyback architecture,
so a low-pass filter (R3 and C
needed. This filter has an extra inverted zero due to R
prove the phase margin of the loop. The 1 mF capacitor is con­nected between V

and the 0.25 Ω sense resistor. To provide

OUT

additional decoupling to ground, a 220 µF capacitor is also con-
nected to V
put capacitor was selected for lowest cost instead of lowest
ripple. Most of the ripple current is shunted by the parallel bat­tery, if connected. If needed, high frequency ringing caused by
circuit parasitics can be damped with a small RC snubber across
the rectifier.

The V

CC

. Output ripple voltage is not critical, so the out-

OUT

source to the ADP3810/ADP3811 can come from a di­rect connection to the battery as long as the battery voltage re­mains below the specified 16 V operating range. If the battery

) on the current sense signal is

C2

C2

voltage is less then 2.7 V (e.g., with a shorted battery, or a bat­tery discharged below it’s minimum voltage), the ADP3810/
ADP3811 will be in Undervoltage Lock Out (UVLO) and will
not drive the optocoupler. In this condition, the primary PWM
circuit will run at its designed current limit. The V
ADP3810/ADP3811 can be boosted using the circuit shown in
Figure 23. This circuit keeps V

above 2.7 V as long as the

CC

of the

CC

–9–

to im-

ADP3810/ADP3811

battery voltage is at least 1.5 V with a programmed charge cur­rent of 0.1 A. For a higher programmed charge current, the
battery voltage can drop below 1.5 V, and V

is still maintained

CC

above 2.7 V. This is because of the additional energy in the
flyback transformer, which transfers more energy through the
10 nF capacitor to V

. The 22 µF bypass capacitor on V

CC

CC

stores the energy transferred through the 10 nF capacitor.

Secondary Side Component Calculations

Design Criteria:

Charging a 6 cell NiCad battery.
Max Individual Cell Voltage: V
Max Battery Stack Voltage: V
Max Charge Current: I
Max Control Voltage: V
R

Fixed Value: R

S

CELLMAX
OMAX

OMAX

CTRL
S

= 1.67 V

= 6 × 1.67 V = 10 V

= 1 A

= 1 V (for I

= 20 kΩ

OMAX

= 1 A)

Pick a Value for R1: R1 = 80.6 kΩ
The voltage limit of 10 V is approximately 10% above the maxi-

mum fully charged voltage when –∆V/∆t termination is used.
This limit gives a second level of protection without interfering
with –∆V/∆t charge termination.

Component Value Calculations:

Current Sense Resistor: RCS = V

CTRL

/(4 × I

) = 1/(4 × 1)

OMAX

= 0.25 W, 1%, 0.5 W

Battery Divider, R2: R2 = V

REF

× R1/(V

OMAX–VREF

)

R2 = 2 × 80.6 kΩ/(10 V–2 V) =

20.15 kΩ, Pick 20.0 kΩ

The final voltage and charge current accuracy is dependent
upon the resistor tolerances. Choose appropriate tolerances for
the desired accuracy. One percent accuracy is recommended.

Charger Performance Summary

The charger circuit properly executes the charging algorithm ex­hibiting stable operation regardless of battery conditions, includ­ing an open circuit load. The circuit can charge to other battery
voltages by modifying only the battery voltage sense divider. As
would be expected, circuit efficiency is best at high battery volt­ages. Replacing the output blocking rectifier diode with a
Schottky would improve efficiency if the Schottky’s leakage
could be tolerated, and its reverse voltage rating met the appli­cation requirement.

1.0

0.9

0.8

0.7

0.6

0.5

LIMIT

I

0.4

0.3

0.2

0.1

0.0

V

= 1.0V

CTRL

V

= 0.5V

CTRL

V

= 0.25V

CTRL

V

= 0.125V

CTRL

2113

45678910

V

OUT

The Battery Charge Current vs. Battery Voltage characteristics
for four different charge current settings are given in Figure 24.
The high gain of the internal amplifiers ensures the sharp transi­tion between current mode and voltage mode regardless of the
charge current setting. The fact that the current remains at full
charging until the battery is very close to its final voltage ensures
fast charging times.

The transient performance for various turn-on and turn-off con­ditions is detailed in Figures 25, 26 and 27. Figure 25 shows
the output voltage when power is applied with no battery con­nected. As shown, the output voltage quickly rises and over­shoots its set voltage. The internal comparator responds to this
and clamps the voltage giving a quick recovery. Without the in­ternal comparator, an external zener would be required to clamp
the voltage to the LED anode. Figure 26 shows the battery cur­rent when connecting and disconnecting a battery. The actual
trace shown is the voltage across R

, which is negative for cur-

CS

rent flowing into the battery. There is an overshoot when the
battery is connected, but the loop quickly takes control and lim­its the average current to the programmed 0.75 A. When the
battery is removed, the current quickly returns to zero. The
solid band on the scope is due to the current rising and falling
with the switching of the PWM. The time scale is too slow to
show the detail of this. Figure 27 shows the output voltage
when a battery stack charged to 6 V is connected and then dis­connected. As expected, when the battery is connected, the
voltage immediately goes to 6 V. When the battery is discon­nected, the voltage returns to the programmed float voltage of
10 V. Again, a small overshoot is present that is clamped by the
internal comparator.

TA = +258C
NO BATTERY

100

10V

VIN = 220V

90

10

0%

0V

2V/DIV

AC

0.1sec/DIV

Figure 25. Flyback Charger Output Voltage Transient at
Power Turn On, No Battery Attached

0.0V

100

90

–200mV

TA = +258C

= 0.775V

V

CTRL

= 220V

V

IN

10

0%

0.2V/DIV

AC

20msec/DIV

Figure 24. Charge Current vs. Battery Voltage at Four Set­tings for the Flyback Charger in Figure 23

Figure 26. Charge Current Transient Response to Battery
Connect/Disconnect

–10–

REV. 0

10V

100

90

6V

10

0%

0V

TA = +258C

= 220V

V

IN

V

= 1V

CTRL

AC

50msec/DIV2V/DIV

Figure 27. Output Voltage Transient Response to Battery
Connect/Disconnect

NONISOLATED TOPOLOGIES
Buck Switching Regulators

The ADP3810/ADP3811 and the ADP1148 can be combined
to create a high efficiency buck regulator battery charger as
shown in Figure 28. The ADP1148 is a high efficiency, synchro­nous, step-down regulator that controls two external MOSFETs
as shown. Similar to the previous flyback circuit, the ADP3810
controls the average charge current and the final battery voltage,
and the ADP1148 controls the cycle by cycle current. The fol­lowing discussion explains the functionality of the circuit but
does not go into detail on the ADP1148. For more information,
the ADP1148 data sheet details the operation of the device and
gives formulas for choosing the external components.

The resistor R

sets the cycle by cycle current limit to 1.5 A,

SENSE

which is far enough above the 1 A average current of the
ADP3810 loop to avoid interfering but still provides a safe
maximum current to protect the external components. The
ADP3810 uses a 0.25 Ω resistor, R
rent. As before, a 20 kΩ resistor is needed between R
V

input of the ADP3810. The RC network from VCS to ground

CS

, to sense the battery cur-

CS

and the

CS

performs the dual function of filtering and compensation.
The voltage loop directly senses the battery voltage. Since the

ADP3810 is used in this circuit instead of the ADP3811, V

SENSE

is connected directly to the battery. The internal resistors set the
battery voltage to 8.4 V in this case. Of course, other voltage

ADP3810/ADP3811

options could be used, or the ADP3811 could be substituted
with external resistors for a user set voltage. Notice the two
grounds in the circuit. One ground is for the high current re­turn to the V
circuitry. R
keep them separate as shown.

The adjustable version of the ADP1148 is used in this circuit in­stead of a fixed output version. The output voltage is fed back
into the V
Doing so provides a secondary, higher voltage limit without
interfering with normal circuit operation. The control output of
the ADP3810 is connected through a 560 Ω resistor to the
SENSE+ input of the ADP1148. The current, I
dc level on the SENSE+ pin, which is added to the current
ramp across R
SENSE+ and reduces the duty cycle of the 1148, giving nega­tive feedback.

The circuit as shown can quickly and safely charge LiIon batter­ies while maintaining high efficiency. The efficiency of the
ADP1148 is only degraded slightly by the addition of the
ADP3810 and external circuitry. The 1.5 mA of supply current
lowers the overall efficiency by approximately 1%–2% for maxi­mum output current. The 0.25 Ω sense resistor further lowers
the efficiency due to the I
rents. See the efficiency discussion in the ADP1148 data sheet
for more information.

Linear Regulator

A third charging circuit is shown in Figure 29. In this case, the
switching supply is replaced with a linear regulator. The ADP3811
drives the gate of an N-channel MOSFET using an external
2N3904. As before, the ADP3811 senses the charge current
through a 0.25 Ω resistor. When the current increases above the
limit, the internal GM amplifier causes the output to go high.
This puts more voltage across R8, increasing the current in Q1.
As the current increases, the gate of M1 is pulled lower, reduc­ing the gate to source voltage and decreasing the charge current
to complete the feedback loop. Because the ADP3811 has a
current output, an external 1 kΩ resistor is needed from the
OUT pin to ground in order to convert the current to a voltage.

source and the other ground for the ADP3810

IN

separates the two grounds, and it is important to

CS

pin, which is set to regulate at V

FB

SENSE

. Higher I

2

increases the voltage on

OUT

× R

power loss at high output cur-

CS

BAT MAX

+ 0.5 V.

, adjusts the

OUT

(0V TO 1V)

REF & CTRL

REV. 0

+V

IN

V

REF

V

CTRL

RTN

V

RTN

0.1µF

0.1µF

IN

* COILTRONICS CTX-68-4
** KRL SL-1-C1-0R068J

V

V

REF

V

SENSE

CTRL

GND

0.1µF

V

CC

ADP3810

COMP

V

IN

P DRIVE

V

SENSE+

SENSE–

N DRIVE

75kΩ

FB

OUT

V

R
2kΩ

C
1µF

1µF

0V = NORMAL

>1.5V = SHUTDOWN

CS

R

C2

560Ω

C

C2

220nF

C1

C1

20kΩ

68pF

C

T

SHUTDOWN

ADP1148

C

T

S GND P GND

Figure 28. High Efficiency Buck Battery Charger

–11–

C

IN

100µF

560Ω

P CH
IRF7204

10
kΩ

1000pF

N CH
IRF7403

L*

62µH

100Ω

100Ω

D1
10BQ040

0.25Ω

R

**

SENSE

50 mΩ

V

BAT

BATTERY

C

OUT

220µF

R

CS

ADP3810/ADP3811

+V

IN

V

REF

V

CTRL

V

&

CTRL

RTN

V

REF

V

IN

RTN

80.6kΩ

R2

20kΩ

ADP3811

GND

0.1µF

V

CC

OUT

V

CS

COMP

R

C1

200Ω
C

C1

1µF

R1

V

SENSE

V

0.1µF

0.25Ω*

V

REF

CTRL

0.1µF
R

C2

560Ω

C

C2

220nF

20kΩ*

1µF

R8
1kΩ

10kΩ

2N3904

250Ω

220µF

V

BAT

Figure 29. ADP3811 Controlling a Linear Battery Charger

IRF7201

1kΩ

R1

= 2.0V ( –– + 1)

R2

V

BAT

BATTERY

The trade-off between using a linear regulator as shown versus
using a flyback or buck type of charger is efficiency versus sim­plicity. The linear charger in Figure 29 is very simple, and it
uses a minimal amount of external components. However, the
efficiency is poor, especially when there is a large delta between
the input output voltages. The power loss in the pass transistor
is equal to (V

IN–VBAT

) × I

. Since the circuit is powered

CHARGE

from a wall adapter, efficiency may not be a big concern, but the
heat dissipated in the pass transistor could be excessive.

An important specification for this circuit is the dropout voltage,
which is the difference between the input and output voltage at
full charge current. There must be enough voltage to keep the
N-channel MOSFET on. In this case, the dropout voltage is
approximately 2.2 V for a 0.5 A output current. Two alternative

ADP3811

V

V

REF

IN

10kΩ

IRF7205

1kΩ

2N3904

V

BAT

ADP3811
OUT

V

ADP3811

OUT

IN

10kΩ

250Ω

2N3904

2N3904

2N5058

1kΩ

V

BAT

a. P-Channel MOSFET b. NPN Darlington

Figure 30. Alternative Pass Transistor for Linear Regulator

realizations of the pass element are shown in Figure 30. In case
(a), the pass transistor is a P-channel MOSFET. This provides
a lower dropout voltage so that V
dred millivolts of V

. In case (b), a Darlington configuration of

IN

can be within a few hun-

BAT

two npn transistors is used. The dropout voltage of this circuit
is approximately 2 V for a 0.5 A charge current.

STABILIZATION OF FEEDBACK LOOPS

The ADP3810/ADP3811 uses two transconductance error am­plifiers with “merged” output stages to create a shared compen­sation point (COMP) for both the current and voltage loops as
explained previously. Since the voltage and current loops have
significantly different natural crossover frequencies in a battery

charger application, the two loops need different inverted zero
feedback loop compensations that can be accomplished by two
series RC networks. One provides the needed low frequency
(typical f
other provides a separate high frequency (f

< 100 Hz) compensation to the voltage loop, and the

C

~ 1 kHz–10 kHz)

C

compensation to the current loop. In addition, the current loop
input requires a ripple reduction filter on the V

pin to filter

CS

out switching noise. Instead of placing both RC networks on the
COMP pin, the current loop network is placed between V
ground as shown in Figure 23 (C

and R

C2

. Thus, it performs

C2)

CS

and

two functions, ripple reduction and loop compensation.

Loop Stability Criteria for Battery Charger Applications

1. The voltage loop has to be stable when the battery is
removed or floating.

2. The current loop has to be stable when the battery is being
charged within its specified charge current range.

3. Both loops have to be stable within the specified input source
voltage range.

Flyback Charger Compensation

Figure 31 shows a simplified form of a battery charger system
based on the off-line flyback converter presented in Figure 23.
With some modifications (no optocoupler, for example), this
model can also be used for converters such as a Buck Converter
(Figure 28) or a Linear Regulator (Figure 29). GM1 and GM2
are the internal GM amplifiers of the ADP3810/ADP3811, and
GM3 is the buffered output stage that drives the optocoupler.
The primary side in Figure 23 is represented here by the “Power
Stage,” which is modeled as GM4, a linear voltage controlled
current source model of the flyback transformer and switch.
The “Voltage Error Amplifier” block is the internal error ampli­fier of the 3845 PWM-IC (R

= 3.3 kΩ in Figure 23), and it is

F

followed by an internal resistor divider. The optocoupler is
modeled as a current controlled current source as shown. Its
output current develops a voltage, V

, across RF. The gain val-

X

ues of all the blocks are defined below.
This linear model makes the calculation of compensation values

a manageable task. It also has the great benefit of allowing the
simulation of the ac response using a circuit simulator, such
as PSpice or MicroCap. For computer modeling, the GM

–12–

REV. 0

ADP3810/ADP3811

GM4

C

V

CTRL

1.0V

1nF

OUT

F1

∆V

C

R

V

A

X

= 0.33V/V

V2

VOLTAGE ERROR

AMPLIFIER

POWER
STAGE

2R

COMP

C

R

3.3kΩ

V

FB

F

1nF

+5V

OPTO COUPLER

ITX

= 0.36mA/mA

OC

F

Figure 31. Block Diagram of the Linearized Feedback Model

amplifiers are represented by voltage controlled current sources,
the optocoupler by a current controlled current source, and the
error amplifier by a voltage controlled voltage source.

Design Criteria

Charging a 6 cell NiCad battery.
Max Battery Stack Voltage: V
Max Charge Current: I
R

Fixed Value: R

S

= 6 × 1.67 V = 10 V

OMAX

= 1 A

OMAX

= 20 kΩ

S

Pick a value for R1: R1 = 80.6 kΩ
Calculated Current Sense

Resistor: R

= 0.25 Ω

CS

Calculated Voltage Sense

Divider: R2 = 20 kΩ

Output Filter Cap: C
2nd Filter Cap: C

= 1 mF (ESR = 0.1 Ω)

F1

= 200 µ F (ESR = 0.2 Ω)

F2

Gain of Each Block

ADP3810/ADP3811

V

Input: GM1 = 8.3 mA/V

CS

ADP3810/ADP3811

V

Input: GM2 = 2.1 mA/V

SENSE

ADP3810/ADP3811

Output Buffer: GM3 = 6 mA/V
Optocoupler: ITX
Voltage Error Amplifier: A

Power Stage (General): GM4 =

= 0.36 mA/mA

oc

= ∆V

V2






C/VX

∆I

∆V

= 0.333



OMAX





C

V

OMAX

I

OMAX×RLOAD

Power Stage

(Voltage Loop): GM4 = 0.091 A/V
Power Stage

(Current Loop): GM4 = 1.0 A/V
The gains for the ADP3810/ADP3811 GM amplifiers are based

on typical measurements of the IC’s open-loop gain, and they
are expressed in units of milliamps per volt. The dc voltage gain

V

BAT

R1

R4

1.2kΩ

80kΩ

GM3

6mA/V

20kΩ

C

CS

GM1

C

C2

0.2µF

R5
400kΩ

220µF

ADP3810/

ADP3811

R

0.25Ω

R3

R

C2

300Ω

V

CS

8.3mA/V

R6
200Ω

80.6kΩ

F2

R2
20kΩ

2.0V

COMP

R

C1

C

C1

V

SENSE

GM2

2.1mA/V

BATTERY

of these stages is the value of GM times the load resistance. At the
COMP pin, the internal load resistance, R5, is typically 400 kΩ.
The optocoupler gain is the typical value taken from the
MOC8103 data sheet. The voltage error amplifier gain is due
to the resistor divider internal to the 3845 only. V

is the out-

X

put of the internal amplifier, as labeled in Figure 31. The actual
op amp is assumed to have sufficient open-loop gain and band­width compared to the system bandwidth; as a result, it can be
considered an ideal transimpedance amplifier. The pole created
by the 1 nF capacitor in parallel with R

is high enough in fre-

F

quency to not affect the compensation.
The power stage gain equation is linearized based on primary

side current mode control with the flyback transformer operat­ing with discontinuous inductor current. ∆I
mum change in output current, which is equal to I
Since the minimum current is 0.0 A, ∆I

OMAX

is the maxi-

OMAX

= I

OMAX

OMAX–IOMIN

= 1 A. The

.

maximum change in control voltage is set by internal circuitry
within the 3845 to ∆V

= 1 V. The load resistor, R

C

LOAD

, is dif­ferent for the voltage and current loop cases. For the voltage
loop without the battery, the effective load is R4, but for the
current loop, the effective load is R

. In the current loop, the

CS

voltage limit has not been reached, so the maximum output
voltage is equal to the maximum output current times the load
resistor. Thus, the entire expression under the square root re­duces to 1.0. Substituting these values into the general equation
for the power stage yields the specific gain values shown for
GM4.

When calculating the loop gain for the voltage loop and the cur­rent loop, there are two main differences. First, GM2 applies
only to the voltage loop, and GM1 applies only to the current
loop. Use the appropriate GM input stage for the particular
loop calculations. Second, there are three battery conditions to
consider. For the current loop, the battery is present and un­charged. Thus, the battery is modeled as a very large capaci­tance (greater than 1 Farad). For the voltage loop, the battery is

REV. 0

–13–

ADP3810/ADP3811

fP1=

f

CV

10

G

LOSS

10











−1

=1. 3 Hz

either present or absent. If the battery is present, its large ca­pacitance creates a very low frequency dominant pole, giving a
single pole system. The more demanding case is when the bat­tery is removed. Now the output pole is dependent upon the
filter capacitors, C

and CF2. This pole is higher in frequency,

F1

and more care must be taken to stabilize the loop response. All
three cases are described in detail below.

The following calculations for compensation components help
to realize stable voltage and current loops. In practical designs,
checking the stability using a network analyzer or a Feedback
Loop Analyzer is always recommended. The calculated compo­nent values serve as good starting values for a measurement­based optimization. The component values shown in Figure 23
are slightly different from the calculated values based on this
optimization procedure.

To simplify the analysis further, the loop gain is split into two
components: the gain from the battery to the ADP3810/
ADP3811’s COMP pin and the gain from the COMP pin back
to the battery. Because the compensation of each loop depends
upon the RC network on the COMP pin, it is a convenient
choice for dividing the loop calculations.

Definitions:

Modulator Gain: G

Error Amplifier: G
Loop Gain: G
Modulator Pole: f

= gain in dB from the COMP pin to

MOD

V

.

BAT

= gain in dB from V

EA

= G

LOOP

, The pole present at the output of the

PM

MOD

+ GEA.

to the COMP pin.

BAT

modulator.

Modulator Zero: f

, The zero due to the ESR, RF1, of the

ZM

filter cap, C

.

F1

Voltage Loop Compensation, No Battery
Step 1. Calculate the dc loop gain (G

G

=20 ×log GM3 ×ITXOC×RF× A

MOD

G

= 20 ×log

MOD

GEA=20 ×log

G

fPM=

2π×R4× C

fZM=

2π×R

[]



6 mA / V ×0.36 × 3.3 kΩ×



0.333 ×0.091 A /V ×1. 2 k Ω







GEA=20 ×log



20 kΩ



80 kΩ+20 kΩ



= 44.5 dB + 48.3 dB = 96.8 dB

LOOP

1

()

F1+CF2

1

F1×CF1

R2



R1+ R2



×2.1 mA /V ×400 kΩ

=

2π×1. 2 k Ω× 1. 2 2 mF

=

2π×0.1Ω×1. 0 mF

), fPM, and fZM:

LOOP

×GM 4 ×R4

V 2



= 48.3 dB






×GM2 × R5

1











=48.5 dB

=0.11 Hz

()

1

=1. 6 kHz

In reality, the interaction of CF1 and CF2 and their ESRs create
an additional pole/zero pair, but because the value of R
of C

) and RF2 (ESR of CF2) are similar, they tend to cancel

F1

(ESR

F1

each other out. Furthermore, the loop crossover is an order of
magnitude lower in frequency, so the additional pole and zero
have little effect on the loop response.

Step 2. Pick the voltage and current loop crossover frequen­cies, f

and fCI:

CV

To avoid interference between the voltage loop and the current
loop, use f
rent loop crossover f
fast current limiting response time, so pick f

Step 3. Calculate G

< 1/10 of fCI, the current loop crossover. The cur-

CV

is chosen to be ~ 1.9 kHz to provide a

CI

MOD

at fCV:

~ 100 Hz.

CV

The modulator gain of 46.7 dB is the dc gain. The modulator
pole reduces this gain above f

G

(100 Hz) =G

MOD

G

(100 Hz) =48.3dB −20 ×log 1+

MOD

.

PM

(dc) −20 × log 1+

MOD



100



0.11





f

CV



f



PM

2



=−10.9 dB





2






Step 4. Calculate gain loss of GEA at fCV:

To have the feedback loop gain cross over 0 dB at fCV = 100 Hz,
G

(100 Hz) should be +10.9 dB. Thus, the total gain loss of

EA

G

needed at crossover is:

EA

= GEA (dc) – GEA (100 Hz) = 48.5 dB – 10.9 dB = 37.6 dB

G

LOSS

Step 5. Determine fP needed to achieve G

To achieve this G

we need to add a pole, which is located at

LOSS

LOSS

:

the COMP pin. GM2 has practically no parasitic loss in
gain at 100 Hz. Its first parasitic pole occurs at approximately
500 kHz as shown in Figure 11. Thus, the entire gain loss must
be realized with an external compensation capacitor, C
sets the pole, f

.

P1

C1

, that

Step 6. Calculate CC1 based upon fP:

CC1=

1

2π×R5× f

≈0.3 µF

P1

Step 7. Calculate the loop phase margin, FM:

The loop phase margin is a combination of the phase of the
modulator pole and zero and the error amplifier pole.

ΦM=180 −arc tan





f

CV

−arc tan





f





P1





f

CV

+arc tan





f





PM





f

CV

≈0°





f





ZM

Step 8. Calculate RC1 to stabilize the loop:

The sum of phase losses of the modulator and error amplifier re­sults in a loop phase of 0°, which is unacceptable for loop stabil­ity. To stabilize the feedback loop, we have to add a phase
boosting zero to the error amplifier by inserting a resistor (R
in series with the capacitor C

φ

= 60 degrees, the frequency of the zero can be calculated:

M

= fCV/tan φM = 57 Hz

f

Z1

From this, the R

resistor is calculated:

C1

RC1=

. If the desired phase margin is

C1

1

Z1×CC1

≈10kΩ

2π× f

C1

)

–14–

REV. 0

ADP3810/ADP3811

Step 9. Iterate CC1:

Because fZ1 is very close to fCV, it will increase the error ampli­fier gain in a nonnegligible amount at the 0 dB point. The in­crease in gain is calculated as:

2





f

20 ×log 1+

Z1





=7.1dB



f



CV

Now, the total error amplifier gain loss required is:

= 37.6 dB + 7.1 dB = 44.7 dB

G

LOSS

With this, the new f

can be calculated from the equation in

P1

Step 5.

f

= 0.58 Hz

P1

Finally, C

is recalculated using the equation in Step 6.

C1

CC1=

2π×400 kΩ×0.58 Hz

1

≈0.7 µF

Following these steps gives a cookbook method for calculating
the compensation components for the voltage loop. As men­tioned above, these components can be optimized in the actual
circuit. The results of a PSpice

1

analysis of the loop is shown in
Figure 32. The open loop gain of the loop is 108 dB as calcu­lated. The crossover frequency is 100 Hz with a phase margin
of 52°. The graph shows the phase leveling off at 90°. In reality
the phase will continue to fall as higher frequency parasitic poles
take effect.

1

PSpice is a trademark of MicroSim Corporation.

180

90

PHASE – Degrees

0

200

100

0

GAIN – dB

–100

0.01 100k0.1 1 10 100

PHASE MARGIN = 52

FREQUENCY – Hz

0dB CROSSOVER

1k

Figure 32. Voltage Loop Gain/Phase Plots

Voltage Loop Compensation, Battery Present

When the battery has finished charging and is still connected to
the charging circuitry, the system is said to be “floating” the bat­tery. The loop is maintaining a constant output voltage equal to
the battery voltage, and the output current has dropped to
nearly zero. This case is actually the easiest to compensate be­cause the battery’s capacitance creates a very low frequency
dominant pole, giving a single pole response. For example, if the
battery is modeled as a 10 Farad capacitor, the dominant pole
will be 1/(2π × 1.2 kΩ × 10 F) = 0.013 MHz. This very low fre­quency pole causes the system to cross over 0 dB at less than
10 Hz, giving a stable single pole system. The compensation
components have little effect on this response, so no further
calculations are needed for this case.

Current Loop Compensation

Now that the voltage loop compensation is complete, it is time
to add the compensation for the current loop. The definitions
for modulator gain and error amplifier gain are the same as be­fore; but now, the controlling error amplifier is GM1 in Figure
31, as opposed to GM2, for the voltage loop. Otherwise, the
calculations are very similar.

Step 10. Calculate the dc loop gain (G

G

=20 ×log GM3 ×ITXOC×RF× A

MOD

G

=20 ×log

MOD

fPM=

2π× R

fZM=

[]



6 mA /V ×0.36 × 3. 3 kΩ×



0.333 ×1. 0 A / V × 0.25 Ω



GEA=20 ×log GM1 × R5

8.3 mA /V ×400 kΩ

[]

G

= –6.1 dB + 70.4 dB = 64.3 dB

LOOP

1

()

CS+RF1

1

2π×R

F1×CF1

[]

=70.4 dB

=

2π×0.35 Ω×1mF

×C

F1

=

2π×0.1 Ω×1mF

), fPM, and fZM:

LOOP

V 2

=20log

1

1

×GM 4 ×R



=−4.5 dB





=450 Hz

=1. 6 kHz

CS

Step 11. Pick the current loop crossover frequency, fCI:

From Step 2 in the voltage loop calculations, fCI ~ 1.9 kHz.

Step 12. Calculate G

MOD

at fCI:

The modulator gain of –4.5 dB is the dc gain. The modulator
pole reduces this gain above f

G

= 1. 9 kHz

()

MOD

G

MOD

=G

dc

()

MOD

= 1. 9 kHz

()

=−4.5 dB−12.7 dB +3.8 dB = –13.4 dB

.

PM

−20 × log 1+



f



f



PM

2



CI

+20 ×log 1+




2





f

CI





f





ZM

If the 1 mF capacitor has a much higher ESR, e.g., 1 Ω, the
modulator zero, f
lator pole, f

PM

, will be lower in frequency than the modu-

ZM

. This causes the loop gain and bandwidth to in­crease and could cause instability. One possible solution to this
scenario is to use a much higher value (47 nF) for the C

= 1 nF

F

capacitor. The pole of this capacitor would then be in the 1 kHz
range and would reduce the loop gain. If the ESR is much less
than 0.1 Ω, the bandwidth of the loop will decrease slightly.

Step 13. Calculate gain loss of GEA at fCI:

The gain loss of GEA in the current loop is a combination of the
loss due to C
calculate the contribution of gain roll-off needed from C
the effective gain of G
is calculated at 1.9 kHz, the impedance of C

, RC1 and the additional loss from CC2, RC2. To

C1

must first be calculated. Since the gain

EA

is 120 Ω. Thus,

C1

C2

, RC2,

the gain becomes:

GEA1. 9 kHz

()

GEA1. 9 kHz

()

G

= G

LOSS

=20 ×log GM1× R6 +RC1+120 Ω

=20 ×log 8.3 mA /V × 10320 Ω

(1.9 kHz) – G

EA

[]

()

[]

()

(1.9 kHz)

MOD

=38.9dB

= 38.9 dB – 13.4 dB = 25.5 dB

REV. 0

–15–

ADP3810/ADP3811

Step 14. Calculate value of RC2 to realize G

LOSS

:

Assuming that CC2 is a short, RC2 forms a resistor divider with
R3, reducing the loop gain. To calculate R

, simply set the resis-

C2

tor ratio to give an attenuation of 25.5 dB, which is a loss of 1/20.

R3

RC2=

20 −1

=1 kΩ

To provide some margin in the circuit for gain fluctuations in
the various stages, the final value of R

was adjusted down to

C2

300 Ω.

Step 15. Calculate the value of CC2:

To maintain high dc gain, a capacitor, CC2, is connected in se­ries with R
close to f

. The zero provided by this RC network should be

C2

to provide a phase boost at crossover:

CI

fZ2≈1. 9 kHz

CC2=

2π× f

1

Z2×RC2

=

2π×1. 9 kHz ×300 Ω

1

≈200 nF

The pole frequency due to CC2 and R3 can now be calculated
as:

2π×C

1

C2

×R3

=40 Hz

fP2=

Step 16. Check the current loop phase margin:

ΦM=180 −arc tan





f

+arc tan

CI

+arc tan





f





ZM





f

CI





f





P2

ΦM≈115°

+arc tan



f





CI

f

P1



+arc tan









f

CI

−arc tan





f





Z2



f



f



CI

Z3





f

CI





f





PM






The above formula subtracts the phase of each pole and adds
the phase of each zero. The poles and zeros come in pairs, f

P2/fZ2

calculated in Step 15 from CC2/RC2; fPM/fZM calculated in Step 10
due to the output filter cap; and f
the same pole that was calculated in Step 9, and f

due to CC1/RC1. fP1 is

P1/fZ3

needs to be

Z3

recalculated with the addition of the internal 200 Ω resistor as
follows:

fZ3=

2π×C

1

× RC1+R6

()

C1

=78 Hz

The final phase margin of 115° is more than adequate for a
stable current loop. In reality, higher order parasitic poles reduce
the phase margin to significantly less than 115° for a 1.9 kHz
crossover. The same was not the case for the voltage loop be­cause the cross over frequency of 100 Hz was well below the
parasitic poles.

A PSpice analysis of the resulting loop gain and phase for the
values calculated is shown in Figure 33.

180

PHASE MARGIN = 105

100

PHASE – Degrees

0

100

50

0

GAIN – dB

–50

0.01 100k0.1 1 10 100 10k
FREQUENCY – Hz

0dB CROSSOVER

1k

C2203–12–10/96

0.1574 (4.00)

0.1497 (3.80)

PIN 1

0.0098 (0.25)

0.0040 (0.10)

SEATING

PLANE

Figure 33. Current Loop Gain/Phase Plots

OUTLINE DIMENSIONS

Dimensions shown in inches and (mm).

8-Lead Small Outline IC

(SO-8)

0.1968 (5.00)

0.1890 (4.80)

8

5

0.2440 (6.20)

41

0.2284 (5.80)

0.0500
(1.27)

BSC

0.0688 (1.75)

0.0532 (1.35)

0.0192 (0.49)

0.0138 (0.35)

0.0098 (0.25)

0.0075 (0.19)

0.0196 (0.50)

0.0099 (0.25)

8°
0°

0.0500 (1.27)

0.0160 (0.41)

x 45°

PRINTED IN U.S.A.

–16–

REV. 0