Page 1

AGO Field Manual
Dartmouth College LF-HF Receiver
May 10, 1996
Page 2

1 I
ntroduction
Many studies of radiowave propagation have been performed in the LF/MF/HF radio
bands, but relatively few systematic surveys have been made of natural emissions in this
part of the spectrum. The predominance of man-made signals in this frequency range
requires a remote location and a radio receiver of specialized capabilities in order to
search for natural emissions. For instance, a receiving system must be capable of both
detecting very weak signals, and be able to step around or null out the known sources of
interference, such as AM broadcast stations. Furthermore, a receiving system must be
able to operate at remote locations with only limited human intervention.
The Automatic Geophysical Observatory (AGO) receiver was designed to run
unattended for periods as long as one year constrained by severe power and data
acquisition limitations.
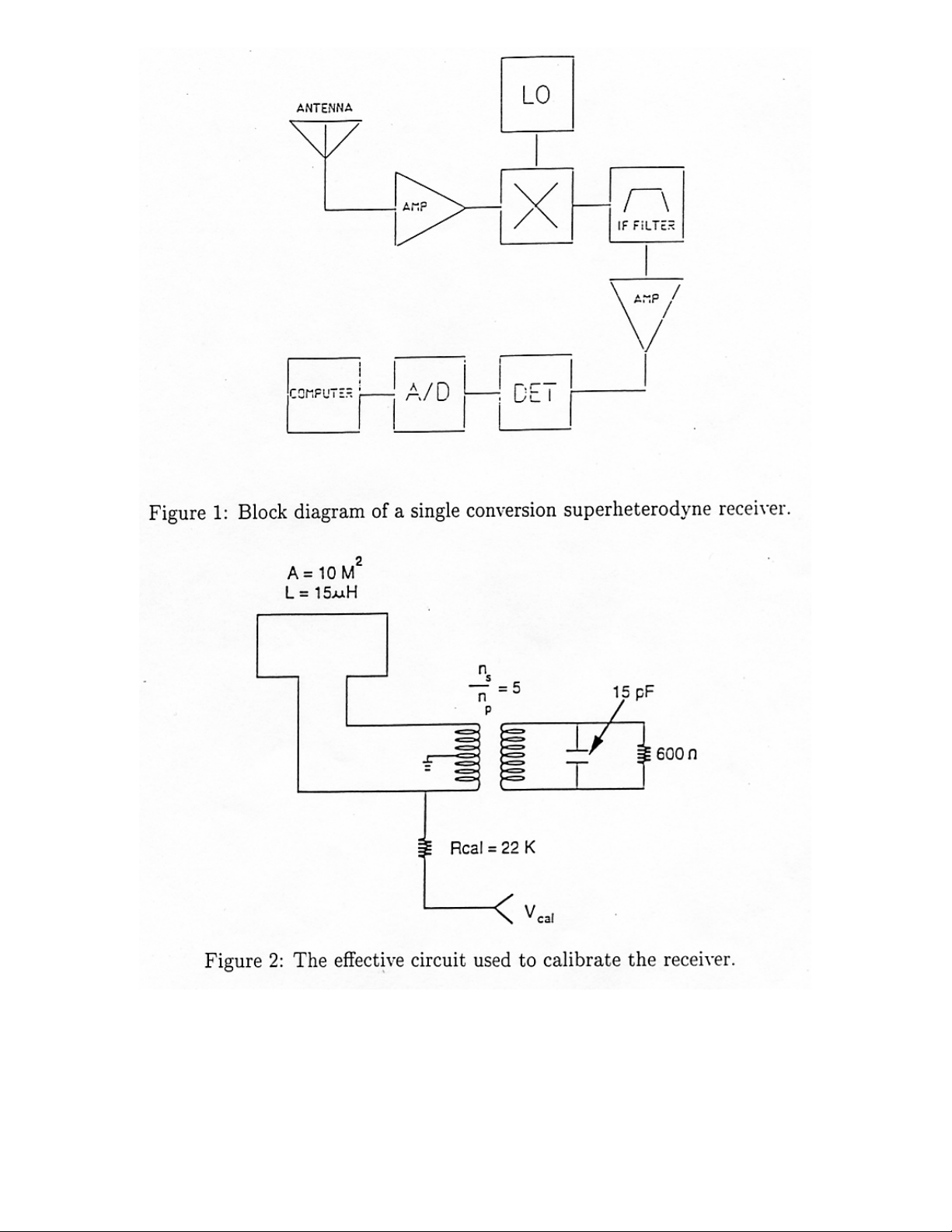
2 Radio Receiving General Principles
The basic components of a single-conversion superheterodyne receiver are shown in
Figure 1. An incoming signal is received by an antenna and amplified before reaching a
mixing stage. At the mixer, the received signal is multiplied or heterodyned with a known
local oscillator (LO) signal to establish an intermediate frequency (IF). In essence, it is
the LO frequency that tunes the receiver to the desired reception frequency. The IF
signal contains frequencies equal to the sum and difference of the frequencies of the LO
signal and the input signal from the antenna. The difference frequency is selected using a
tuned IF crystal filter. The resulting signal is amplified, detected, and digitized. There is
no need for an automatic gain control in our receivers since we are looking for absolute
signal strength and are not interested in keeping a constant output, as is typically
desirable in commercial receivers. Furthermore, receivers with two mixer stages
(double-conversion receivers) are also not desirable since the dynamic range of such a
receiver is usually downgraded through the addition of the second mixer.
1
Page 3
2
Page 4

3 Antenna and Preamplifier
The AGO LF/MF/HF receiver employs a magnetic loop antenna which is less susceptible
to locally generated noise than an electric dipole, especially when oriented to null out the
strongest local signal. The loop consists of a single turn of wire arranged in a square
between two vertical 12-foot-long 4 x4 posts placed 3 m apart. One horizontal wire
runs along the snow, and the other connects the tops of the posts, so that the area of the
loop antenna is 10 square meters. Figure 3 shows the antenna as deployed at AGO-P2.
The preamplifier is buried in the snow at the base of the antenna, with a pole or
flag installed to make it easy to retrieve. A schematic of the most recent version of the
preamplifier is included in the schematics portion of this manual. A critical component
of the preamplifier is the calibration circuit, which allows the absolute level of the
received signals to be calibrated. For this purpose, a broadband calibration signal
designed to be near the top of the instrument s range is injected approximately hourly.
This signal is detected by the receiver with its nominal gain, and then detected with the
gain reduced by 20 dB. Using both of these detections, the gain and offset of the
instrument can be accounted for, and the signals from the various AGO s can be
compared. Figure 2 shows the effective calibration circuit. (The 600-Ohm resistor
represents the input impedance of the preamplifier.)
The voltage at the antenna terminals of the loop antenna is related to the electric
field of the impinging EM radiation:
dE
A
V =
(1)
dt
c
where A is the antenna area (10 m2), E is the electric field strength, and c is the velocity
of light. Assuming that the antenna can be considered a perfect inductor at the
frequencies of interest,
dI
LV =
dt
(2)
where I is the current in the antenna, this leads to the following relation after integration
LI =
A
E
c
(3)
3
Page 5

Figure 1: The 10 m2 loop antenna installed at AGO-P2, Antarctica. The AGO facility,
along with two Scott tents, can be seen in the background. The preamplifier is buried
several feet under the checkered flag in order to keep it at a constant temperature.
4
Page 6

If a ca
lib
RVI
ration resistor R
is placed in series with the antenna such that
cal
calibration voltage (voltage at the antenna terminals) becomes
AR
cal
E
cL
For our 10
V
=
cal
2
loop antenna, the electric field strength (V/m) and V
following equation,
=
calcal
(4)
are related through the
cal
, the
VE 01.0=
cal
(5)
which was obtained by substituting the appropriate measured quantities into the above
equations.
The least detectable signal of this receiving system corresponds to
cal
50≈
.
VV
µ
Therefore, the power spectral density of the received signal at the loop antenna is
1
/5 mHznV
2
, assuming a 10 kHz bandwidth.
4 Receiver
The AGO LF/MF/HF receiver is located in the observatory, 300-500 feet distant from the
antenna. Figure 4 shows a block diagram of the AGO receiver. Power from the DAU
comes in on the specified connector and is converted to the required ±10 Volts and ±5
Volts DC on the power supply board. The mixing of the signals occurs on the receiver
board; the LO signal used in the mixing is produced on the local oscillator board. The
signals are compressed and prepared for the DAU on the compression board.
The receiver is tuned by adjusting the frequency of the LO signal. The sequence
of frequencies to be tuned is programmed into an erasable programmable read only
memory chip (EPROM), which is then clocked at the desired frequency-switching rate. In
the AGO s, this EPROM is actually clocked at 20 Hz, twice the rate at which bytes are
actually transferred to the DAU. The receiver compresses samples by a factor of two and
passes one byte to the DAU each 0.1 s which most of the time represents two samples.
The EPROM contains a sequence of 72000 steps, which are clocked at 20 Hz to control
one hour of measurements. At the end of the hour, the EPROM is reset, and the cycle
repeats. (The EPROM also contains a test program, to be used only for debugging, which
is enabled by setting one address bit high using a DIP-switch.)
5
Page 7

6
Page 8

Th
e receiver as currently configured measures
116 f
requencies from 30 kHz to
4.5 MHz. The frequencies are not spaced linearly but are arranged to optimize reception
of known natural signals such as auroral hiss and auroral roar. Furthermore, the
frequencies are arranged in two sets of 58 frequencies with each of these subsweeps
ranging from the low end of the frequency range to the high end but consisting of
frequencies slightly offset. Using sub subsweeps provides higher effective time resolution
for detection of relatively broadband signals. Table 1 at the end of this section gives the
list of the 116 frequencies sampled. The 58 frequencies in the left column are sampled
first, then the 58 frequencies in the right column are sampled. The 20-Hz data rate (with
compression) implies that a full sweep of 116 frequencies is obtained each 5.8 s, and a
subsweep of 58 frequencies is obtained each 2.9 s.
Data compression is critical to the performance of the AGO LF/MF/HE receiver.
The compression works by transmitting periodically a reference sweep of 120 bytes
which provides 8-bit measurements of the logarithm of the received signal strength of
each of the 116 frequencies (plus two sync-byte plus two filler bytes). Following the
reference sweep, 44 delta-sweeps are transmitted. In these, only the change in each
signal strength is transmitted, compressed to a 4-bit number. Hence these 44 sweeps are
require only 2640 bytes (44 times 60; two sync-bytes are attached to each delta-sweep).
Following these delta sweeps, another reference is transmitted (which requires 120
bytes), then 44 more delta-sweeps, and so on. Once an hour, a calibration sweep is
performed, consisting of 120 bytes: an 8-bit sample of the calibration signal at each of the
116 frequencies, with the receiver at full gain for even samples and with gain reduced by
20 dB for the odd samples; plus two unique sync-bytes, plus two filler bytes. Thirteen
blocks consisting of a reference and 44 delta-sweeps are transmitted between each
calibration sweep; the result is a package of 36000 bytes transmitted to the DAU every
hour, providing exactly the quantity of data (0.1 byte per second) allotted to the
LF/MF/HF receiver.
All of the numbers cited above — controlling the frequency of reference sweeps,
calibration sweeps, etc. — can be changed by re-programming and replacing the EPROM.
The number of sampled frequencies as well as the actual frequencies sampled may also
be changed this way. If in the future it becomes possible to store a larger quantity of
data, the data rate can easily be increased by up to a factor of ten by adjusting DIP
switches in the unit (without any change of hardware).
7
Page 9

Th
e output of the receiver is available as an analog signal on the front of the
receiver box, and instructions in this manual tell how a two-channel oscilloscope can be
used to produce an image on the screen of power versus frequency. Furthermore, a
computer program has been written for DOS, which decodes the digital output of the
receiver and produces a power-versus-frequency plot on the computer screen, which
updates in real time. To use this program, the digital output of the receiver must be
connected to the serial input of the computer. Figure 5 shows an example of a spectrum
generated using this program in combination with one of the AGO LF/MF/HF receivers
in the lab at Dartmouth. A version of this program is being prepared which will review a
file of LF/MF/HF data extracted from the DAU. If a file can be produced which contains
sequentially the bytes provided by the LF/MF/HF receiver, these bytes can be decoded
and displayed on the screen as power versus frequency, updated either by the operator or
at a rate fixed to the computer clock. All three of these tools will enable the operators in
the field to determine whether the receiver is functioning.
The AGO-based LF/MF/HF receivers should yield the most sensitive
measurements to date in this frequency range. The capability of simultaneous
measurements between several AGO sites also will enable the temporal and spatial
effects of natural LF/MF/HF radio emissions to be studied. Finally, since each AGO will
consist of a core group of synchronized geophysical experiments, correlations between
data sets which are exactly co-located can be easily made.
8
Page 10

9
Page 11

All Frequencies in
kHz
1st Subsweep
30 40
50 60
70 80
90 100
110 120
130 140
150 160
170 180
190 200
210 220
230 240
250 260
270 280
290 300
310 320
330 340
350 360
370 380
390 400
420 440
460 480
500 520
540 560
580 600
620 640
660 680
700 740
780 820
860 900
940 980
1020 1060
1100 1180
1260 1340
1420 1500
1580 1660
1740 1820
1900 1980
2060 2140
2220 2300
2380 2420
2460 2500
2540 2580
2620 2660
2700 2740
2780 2820
2860 2900
2940 2980
3020 3060
3100 3140
3180 3220
3300 3380
3460 3540
3620 3700
3780 3860
3940 4020
4100 4180
4260 4340
4420 4500
2nd Subsweep
Table 1: Sequence of frequencies measured in the current version
of the AGO LF/MF/HF Receiver. The sequence runs down the
first column, then down the second column (116 frequencies total).
10
 Loading...
Loading...